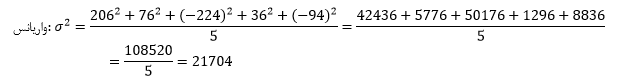نوشتن صحیح و اصولی فرضیات یا سوالات تحقیق یکی از گامهای اساسی و مهم در پیشبرد کار پایان نامه یا تحقیق شماست. تدوین اصولی فرضیه، تشخیص و تفکیک درست فرضیه تحقیق از فرضیه آماری یا فرض صفر مهیا کننده اقدام بعدی در جهت آزمون فرضیه آماری (آزمون فرض آماری) با استفاده از نرم افزار spss و توسط روشها و آزمونهای آماری می باشد.
طراحی پرسشنامه نیز می بایست بر اساس فرضیات تحقیق انجام شود و بگونه ای این کار صورت پذیرد که متغیرهای مذکور در فرضیه توسط ابزار پرسشنامه به درستی اندازه گیری شوند.
چه خوب است که در همان ابتدای کار تدوین فرضیه و طراحی پرسشنامه ، به نتیجه نهایی یعنی آزمون فرضیات آماری نیز نگاهی داشته باشید تا از دوباره کاری ها پرهیز شده و در وقت و انرژی شما صرفه جویی گردد. حالتی را تصور نمایید که فرضیه به درستی تدوین نشده است، یا سوالات پرسشنامه به اندازه گیری و کمی کردن متغیرهای مورد نظر منتهی نمی شود!!
پیشنهاد ما به شما این است که در طی مراحل تحقیق خود با ما به عنوان مشاور آماری مطمئن در تماس و ارتباط باشید (از طریق واتساپ یا ایمیل) تا با گامهای اصولی و درست و مطمئن به هدف خویش در پایان نامه یا تحقیق نائل شوید. انجام آزمون آماری فرضیات تحقیق را می توانید به ما بسپارید یا در این مسیر از مشاوره ما بهره مند گردید.
تدوین فرضیه
پس از انتخاب و نوشتن مسئله باید محقق تصویری ذهنی از چگونگی متغیرها و نحوه ارتباط آنها با یکدیگر ارائه دهد تا بر اساس آن تلاش کاوشگرانه خود را آغاز کند. بنابراین اقدام به تدوین و تبیین قضایای فرضی و پیشنهادی در چهارچوب مساله تحقیق خود می نماید، به نحوی که چگونگی متغیر یا پدیده و نیز روابط آنها را با یکدیگر توضیح دهد.
فرضیه سازی یکی از مراحل حساس تحقیق را تشکیل می دهد؛ چرا که فرضیه ها نقش راهنما را دارند و به فعالیتهای تحقیقاتی جهت می دهند. فرضیه ها به محقق کمک می کنند تا از بین طرق فراوان رسیدن به مقصد تنها چند مورد آن را که بیش از همه نزدیک تر به مقصد به نظر می رسد بر گزیند.
مبادی شکل گیری فرضیه
فرضیه ها در ذهن دانشجویان و محققان ، به صورت انفرادی و یا ترکیبی ، از مبادی زیر پدیدار می شوند و به عنوان سرچشمه پیدایش و شکل گیری فرضیه و گمان علمی در ذهن پژوهشگر عمل می نمایند:
۱- معلومات پیشین که در قالب گزاره های نظری مانند اصول و قوانین علمی، نظریه ها،حقایق، مفاهیم، مدلها و غیره وجود دارند و در شکل ادبیات نظری پژوهش تدوین می شوند.
۲- تجربیات دیگران، نظیر سوابق پژوهشی و تجربی سایرین که درباره موضوع یا مشابه آن وجود دارد.
۳- تجربیات پژوهشگر؛ در محیط واقعی یا در آزمایشگاه
۴- تعامل با دیگران، گفتگو و مصاحبه با صاحب نظران و متخصصان
مفهوم و تعریف فرضیه
در تعریف فرضیه می توان گفت: فرضیه عبارت است از حدس یا گمان اندیشمندانه درباره ماهیت، چگونگی و روابط بین پدیده ها، اشیاء و متغیرها، که محقق را در تشخیص نزدیک ترین و محتمل ترین راه برای کشف مجهول کمک می نماید؛ بنابراین فرضیه گمانی است موقتی که درست بودن یا نبودنش باید مورد آزمایش قرار گیرد.
تفاوت فرضیه با نظریه و قوانین یا معلومات کلی این است که نظریه و قوانین عمدتا مشتمل بر قضایای کلی و عمومی هستندو به مورد خاصی تعلق ندارند و می توانند مصادیق زیادی داشته باشند، در حالی که فرضیه حالت کلی ندارد و مختص مسئله تحقیق است که از قضایای کلی ناشی می شود ولی در قلمرو یک تحقیق خاص شکل می گیرد؛ به همین دلیل، یک محقق نمی تواند فرضیه خود را در تحقیق مورد نظرش به صورت قضیه کلی بیان نماید. هر چند از قضایای کلی به روش قیاسی و از کل به جزء فرضیه سازی می نماید و فرضیه های خود را از قضایای کلی استنتاج می کند، ولی باید مفاهیم و اصطلاحات مربوط به فرضیه را به مساله تحقیق خود یعنی همان مطالعه موردی محدود کند.
نقش فرضیه در تحقیق علمی
فرضیه، توجیه و تبیینهای حدسی معینی را درباره واقعیات عرضه می کند و پژوهشگران را در بررسی این واقعیات و تجارب کمک و هدایت می کند. فرضیه یک پیشنهاد توجیهی و به زبان دیگر راه حل مسئله است که هم به یافتن نظم و ترتیب در بین واقعیات کمک می کند و هم باعث استنتاج می شود.
فرضیه ها ضمن اینکه برای پیگیری و انجام دادن امور تحقیق به طور کلی به محقق جهت می دهند باعث می گردند که :
نخست، مطالعه منابع و ادبیات مربوط به موضوع تحقیق جهت دار شود و از مطالعه منابعی که ربطی به پژوهش ندارند جلوگیری به عمل آید.
دوم، پژوهشگر را نسبت به جنبه های موقعیتی و معنی دار مسئله پژوهش حساس تر می نمایند.
سوم، فرضیه باعث می شود تا محقق مسئله پژوهش را بهتر درک کند و روشهای جمع آوری اطلاعات را بهتر تعیین نماید.
چهارم، فرضیه چهارچوبی برای تجزیه و تحلیل و تفسیر اطلاعات جمع آوری شده و نتیجه گیری از آن ارائه می دهد.
نکته ای که باید به آن توجه شود آن است که تحقیقات علمی از هر نوعی که باشند نیاز به تدوین فرضیه دارند.
در تحقیقات توصیفی فرضیه ها مبین تصویر حدسی از وجود حالات، شرایط، صفات، ویژگیهای اشیاء و اشخاص، موقعیتها، پدیده ها و رخدادهایی هستند که نسبت وقوع رویداد، صفات، ویژگیهای اشیاء و پدیده ها را توضیح می دهد.
در تحقیقات علی و همبستگی فرضیه از وجود رابطه صحبت می کند، چه رابطه های همبستگی و چه رابطه های علّی که مبین رابطه علت و معلولی هستند.
نکته: گاهی اوقات امکان تدوین فرضیه وجود ندارد. مثلا:
۱- طرحهایی که ماهیت مطالعاتی داشته و شبه پژوهش هستند و عمدتا بر پایه اطلاعات و معلومات پیشین و دست دوم تهیه می شوند. مانند، تهیه و تدوین اطلسها، دایره المعارفها، بررسیهای توصیفی، و امثال آن.
۲- برخی پژوهشهای کاربردی که از جنس طراحی هستند، مانند طرح های آمایشی
فرضیه آماری (فرضیه صفر) در مقابل فرضیه تحقیق
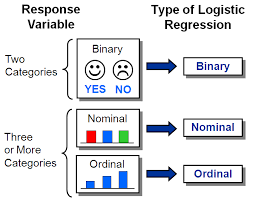
انواع فرضیه در تحقیقات همبستگی و تجربی را به دو نوع تقسیم می کنند: فرضیه تحقیق یا یک (H1: Research Hypothesis) و فرضیه پوچ یا صفر (H0: Null or Statistical Hypothesis) .
فرضیه تحقیق از وجود رابطه یا اثر و یا تفاوت بین متغیرها خبر می دهد یا در واقع وجود این حالات را تایید نموده آن را واقعی و حقیقی می داند. این فرضیه به دو نوع جهت دار و بدون جهت تقسیم می شود.
فرضیه صفر که به فرضیه آماری یا پوچ نیز موسوم است بر خلاف فرضیه تحقیق، وجود رابطه، اثر یا تفاوت بین متغیرها را رد کرده، انکار می نماید و اظهار می دارد که این حالات واقعی نیست و حقیقت ندارد و صرفا ناشی از تصادف و اشتباهات آماری به ویژه در نمونه گیری است.
از فرضیه های مزبور می توان به فرضیه های زوجی نیز تعبیر نمود. یعنی فرضیه مرکب از زوج صفر و یک می باشد.
مثال زیر انواع فرضیه را نشان می دهد:
الف- فرضیه تحقیق جهت دار:
– به نظر می رسد کارایی معلمان آموزش دیده بیشتر از معلمان آموزش ندیده است.
ب) فرضیه تحقیق بدون جهت، در تحقیق مورد نظر:
– به نظر می رسد بین آموزش معلمان و کارایی آنها رابطه وجود دارد.
ج) فرضیه صفر در تحقیق مورد نظر:
– به نظر می رسد کارایی معلمان آموزش دیده و آموزش ندیده مساوی است.
اگر چه محقق فرضیهٔ تحقیق را مطرح می کند و درصدد آزمایش آن است، پس از گردآوری اطلاعات و داده ها و طبقه بندی آنها عملاً فرضیه ی صفر را مورد آزمایش قرار می دهد؛ زیرا روشهای آماری تجزیه و تحلیل داده ها قادر به آزمون فرضیه صفر هستند. البته ممکن است محقق در فرضیات خود اشاره ای به فرضیه ی صفر ننماید، ولی در عمل فرضیهٔ صفر مورد آزمون قرار می گیرد و هر حکمی که در مورد فرضیه صفر پذیرفته شد، محقق می تواند عکس آن را در مورد فرضیه تحقیق به کار گیرد.
مطالعه چگونگی روابط بین متغیرها در یکی از سه حالت زیر انجام می پذیرد:
الف) محقق به دنبال بررسی و مقایسه تفاوت تاثیر دو یا چند متغیر بر یک یا چند متغیر است؛ مانند تفاوت تاثیر دو روش تدریس بر شاگردان.
ب) محقق در پی مطالعهٔ میزان همبستگی بین دو یا چند متغیر است؛ مانند بررسی همبستگی مشکلات روانی و گرایش به اعتیاد.
ج) محقق به دنبال کشف و تعیین رابطهٔ علت و معلولی بین دو یا چند متغیر است؛ مانند تاثیر عامل هوش در پیشرفت تحصیلی.
نکته: فرضیه های زوجی (صفر و یک) مختص پژوهشهایی است که هدف آنها کشف رابطهٔ بین متغیرهاست. نظیر تحقیقات همبستگی و تجربی آزمایشگاهی. بنابراین در تحقیقاتی که کشف رابطه ها مد نظر نمی باشند فرضیه زوجی موضوعیت ندارد و پژوهشگر نسبت به تدوین فرضیه های انفرادی اقدام خواهد نمود. مثلا در تحقیقات توصیفی، تاریخی و پس رویدادی غیر کمی محقق نسبت به تدوین فرضیه های انفرادی اقدام می کند و فرضیه زوجی برای آنها بی معنی است.
ویژگیهای یک فرضیه خوب
۱- فرضیه باید قدرت تبیین حقایق را داشته باشد و واقعیت مسئله یا متغیر یا روابط مورد مطالعه را منعکس کند.
۲- فرضیه باید بتواند پاسخ مساله تحقیق را بدهد. یعنی آنچنان با مسئله تحقیق یا سوالات فرعی مرتبط باشد که اطلاعات گردآوری شده پس از تجزیه و تحلیل، پاسخگوی حل مسئله قابل استفاده باشد.
۳- فرضیه باید قابلیت حذف حقایق نامرتبط با مساله تحقیق را داشته باشد و با سایر سؤالات فرعی و فرضیه های دیگر تداخل نداشته باشد.
۴- فرضیه باید شفاف، ساده و قابل فهم باشد و از در آن از عبارات مبهم، طولانی و دو پهلو استفاده نشود.
۵- فرضیه باید قابلیت آزمون را داشته باشد؛ یعنی مفاهیم و متغیرهای مطرح شده در فرضیه قابل تبدیل به تعاریف عملیاتی و واجد معرفها و شاخصهایی برای اندازه گیری، ارزیابی و سنجش باشند تا بتوان با وسایل و امکانات موجود آن را مورد آزمایش قرار داد.
۶- فرضیه نباید با حقایق و قوانین مسلم و اصول علمی تایید شده مغایرت داشته باشد.
۷- در فرضیه نباید از واژه ها و مفاهیم ارزشی استفاده شود.
۸- فرضیه باید به مطالعه و پژوهش جهت بدهد و راهنمای فعالیتهای محقق باشد.
۹- فرضیه باید به صورت جمله خبری باشد تا از نحوه ارتباط متغیرها خبر بدهد.
۱۰- فرضیهها باید مختص مطالعه موردی مساله تحقیق باشند. بنابراین از تدوین فرضیه های عام و غیر قابل حمل بر مصداق خاص مورد تحقیق باید پرهیز نمود.
۱۱- باید بین فرضیه ها و سوالهای ویژه یا فرعی تحقیق تناظر صوری و محتوایی وجود داشته باشد. فرضیه ها در واقع پاسخهای حدسی به سوالهای فرعی یا ویژه مربوط به تحقیق هستند.
نکته: چنانچه فرضیه های متعدد داشته باشیم، باید این فرضیه ها به گونه ای تنظیم شوند که مجموعا یک واحد کلی و یک سیستم یا دستگاه حدسی را تشکیل دهند و هماهنگ و همسو باشند.
منبع: داده پردازی آماری اطمینان شرق



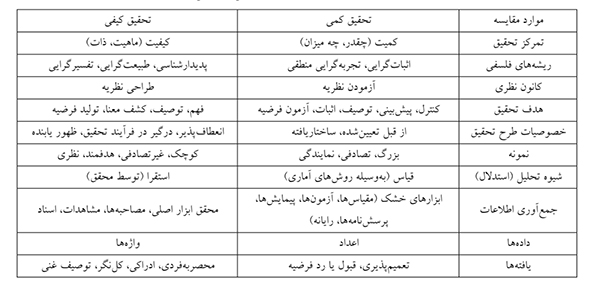





 و
و  است دارای توزیع t با n-1 درجه آزادی است.
است دارای توزیع t با n-1 درجه آزادی است.


 برای محاسبه واریانس، اختلاف تکتک دادهها را به توان دو رسانده و سپس میانگین میگیریم:
برای محاسبه واریانس، اختلاف تکتک دادهها را به توان دو رسانده و سپس میانگین میگیریم: