جستجوی پرسشنامه استاندارد و معتبر همراه با روایی و پایایی

http://porseshname.com

در این سایت خدمات ارائه پرسشنامه های استاندارد، طراحی و تدوین پرسشنامه های محقق ساخته، ویرایش و تنظیم پرسشنامه‌های آماده انجام می‌گیرد.

شرایط و پیش فرض های تحلیل کوواریانس (آنکووا) ANCOVA

هدف از انجام تحلیل کوواریانس

هدف از انجام تحلیل کوواریانس (ANCOVA) در مطالعات کار آزمایی بالینی مقایسه دو گروه کیس و کنترل بعد از مداخله (پس آزمون) با یکدیگر است. در صورتی که اندازه های قبلی (پیش آزمون) کنترل شده باشد. در نهایت تحلیل کوواریانس به این سوال پاسخ می دهد که آیا مداخله موثر و معنی دار بوده است یا خیر ؟

در واقع یکی از راه های کنترل اثرات نمره پیش آزمون به عنوان اثر انتقال، استفاده از آزمون آنالیز کوواریانس (ANCOVA) است. به طوری که شرایطی برای مطالعه فراهم می شود. تا اثرات درمان را جدا از اثر بالقوه نمره پیش آزمون بررسی کند.

تفاوت تحلیل کوواریانس (ANCOVA) و تحلیل واریانس (ANOVA)

آنکووا گسترش داده شده ی آنالیز واریانس است که پیش فرض های آن را نیز دارد. تفاوت آشکار بین ANOVA و ANCOVA حرف “C” است که مخفف “کواریانس” است. مانند ANOVA، “تجزیه و تحلیل کوواریانس” (ANCOVA) یک متغیر پاسخ پیوسته دارد. تحلیل کوواریانس (ANCOVA) مانند تحلیل واریانس برای تشخیص تفاوت در میانگین چند گروه متغیر مستقل، در حالی که کار کنترل متغیرهای کووریت (Covariate Variables) را انجام می دهد، استفاده می شود. متغیر کووریت معمولاً جزئی از سؤال اصلی تحقیق نیست اما می تواند متغیر وابسته را تحت تأثیر قرار دهد و بنابراین باید کنترل شود.

در حالی که آنالیز واریانس به دنبال اختلاف در بین میانگین ها است. تحلیل کوواریانس به دنبال اختلاف میانگین های تعدیل شده (به وسیله متغیر کووریت که به آن متغیر مخدوش کننده نیز می گویند) می باشد.

پیش فرض های تحلیل کوواریانس تک متغیره (ANCOVA)

قبل از معرفی پیش فرض های تحلیل کوواریانس، از این که یک یا چند پیش فرض معرفی شده در هنگام آنالیز دیتا با نرم افزار SPSS رعایت نشود تعجب نکنید ! همیشه داده استخراج شده از دنیای واقعی مانند مثال های موجود در متن کتاب ها همه چیز را مطلوب نشان نمی دهد. همچنین از این که چند پیش فرض اصلی هم رد شود نگران نشوید ! همیشه یک راه حلی باید وجود داشته باشد.

پیش فرض اول : پیوسته بودن متغیر وابسته و کووریت

متغیر وابسته و متغیر کووریت بایستی پیوسته باشد. برای مثال متغیر زمان (که با واحد ساعت اندازه گیری می شود)، نمرات IQ (امتیاز IQ) نمرات امتحان (0 تا 20) و وزن (به کیلوگرم) پیوسته و کمی می باشد. البته متغیرهای کووریت (متغیرهای مخدوش کننده) می تواند رسته ای نیز باشد (مانند جنسیت). که در این حالت آزمون ANCOVA ترجیح داده نمی شود.

پیش فرض دوم : رسته ای بودن متغیر مستقل

متغیر مستقل بایستی شامل دو یا چند سطح باشد برای مثال جنسیت که دارای دو سطح زن و مرد است. همچنین متغیر گروه تحقیق که شامل (گروه کیس و گروه کنترل) است. فعالیت فیزیکی (کم، متوسط، زیاد) نیز مثال دیگری از این قبیل می باشد.

پیش فرض سوم : استقلال مشاهدات

هیچ ارتباطی بین مشاهدات در هر گروه و یا بین گروه ها وجود نداشته باشد. همچنین هیچ یک از شرکت کننده ها (اعضای نمونه) در بیش از یک گروه نباشد. البته این موضوع بیشتر به طراحی مطالعه مربوط می شود. اگر این پیش فرض رعایت نشود نیاز به یک آزمون آماری دیگری به جای آزمون ANCOVA می باشد.

پیش فرض چهارم : عدم وجود داده پرت

در بین داده های پژوهش نباید داده پرت قابل توجهی وجود داشته باشد. چرا که وجود داده پرت ممکن است بر نتایج بدست آمده از تحلیل کوواریانس تاثیر منفی بگذارد و از اعتبار نتایج آن کاهش دهد.

پیش فرض پنجم : نرمال بودن باقی مانده ها

برای هر سطح از متغیر مستقل، باقی مانده بدست آمده تقریبا بایستی دارای توزیع نرمال باشد. به این دلیل از واژه تقریبا استفاده کردیم چون می دانیم این پیش فرض در اکثر اوقات اتفاق نمی افتد در حالی که نتایج بدست آمده از تحلیل کوواریانس معتبر باقی می ماند.

پیش فرض ششم : همگنی واریانس ها

این پیش فرض به کمک انجام آزمون لون (Levene’s test) در نرم افزار SPSS قابل بررسی است.

پیش فرض هفتم : ارتباط خطی کووریت با متغیر وابسته

در هر سطح از متغیر مستقل، متغیر کووریت رابطه خطی با متغیر وابسته دارد. این پیش فرض به کمک نرم افزار SPSS از طریق رسم Scatter plot گروه بندی شده از متغیر کووریت، پیش آزمون متغیر وابسته و متغیر مستقل بررسی می شود.

پیش فرض هشتم : همسانی واریانس

این پیش فرض به کمک نرم افزار SPSS از طریق رسم Scatter plot ار باقی مانده های رگرسیون در مقابل مقادیر پیش بینی شده بررسی می شود.

پیش فرض نهم : همگنی شیب رگرسیون

 همگنی شیب رگرسیون بدین معنی است که شیب رگرسیونی خطوط مختلف در بین گروه ها باید برابر باشد. به عبارت دیگر تعامل نمرات کووریت و متغیر مستقل در بین گروه ها نباید اختلاف معنی داری داشته باشد. به عبارتی دیگر، نیاز هست که شیب های خطوط رگرسیونی برای کووریت ها (در ارتباط با متغیر وابسته) در بین گروه ها (کیس و کنترل) یکسان باشد که به این پیش فرض همگنی شیب رگرسیون گفته می شود که می تواند با یک آزمون F بر روی تعامل متغیرهای مستقل با کووریت ها ارزیابی شود. اگر آزمون F معنادار بود، بدین معنی است که این پیش فرض نقض شده است.

ارائه مثال انجام تحلیل کوواریانس در SPSS

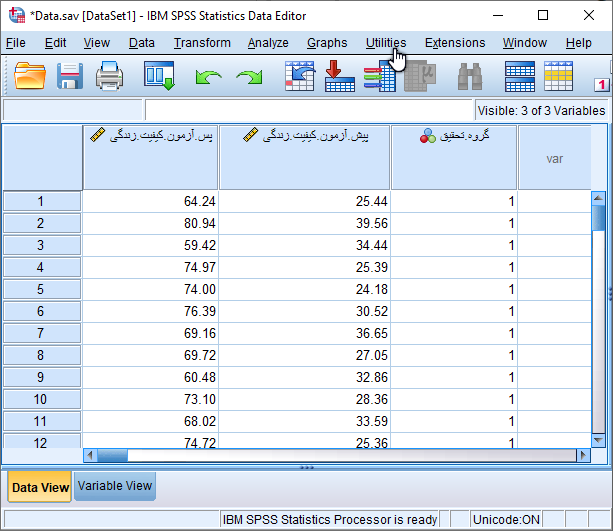
در یک مطالعه ای فرضی، پرسشنامه کیفیت زندگی در اختیار 60 نفر از مبتلایان به صرع شرکت کننده در پژوهش قرار داده شد تا آن را تکمیل نمایند. این 60 نفر به صورت تصادفی به دو گروه 30 (کنترل) و 30 (کیس) تقسیم بندی شدند. بیماران گروه کیس (Case) تحت مداخله (پیگیری تلفنی به صورت برقراری 10 تماس 15 دقیقه ای) در طی دو ماه قرار گرفتند. همچنین، در بیماران گروه کنترل (Control) هیچ گونه مداخله ای انجام نشده و آموزش های روتین را دریافت کردند. پس از دو ماه و حین مراجعه به درمانگاه، کیفیت زندگی در دو گروه کیس و کنترل مجددا مورد بررسی قرار گرفت.

 

نحوه ورود داده برای انجام تحلیل کوواریانس در SPSS

برای سادگی نمایش داده های وارد شده، فقط نمرات کل کیفیت زندگی را قبل و بعد از مداخله مانند شکل زیر در نرم افزار SPSS وارد کرده‌ایم. توجه داشته باشید که نمرات گروه کیس و کنترل در پیش آزمون و پس آزمون بایستی در یک ستون و زیر هم وارد نرم افزار شود و با ایجاد متغیر دو سطحی گروه تحقیق از لحاظ گروه مطالعه قابل تشخیص باشد.

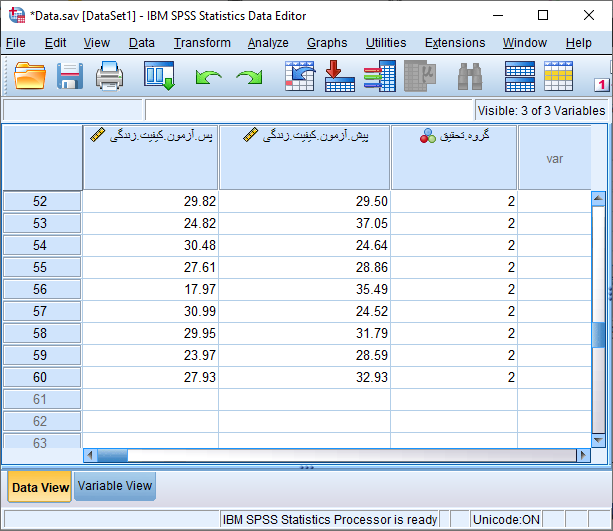
حال دیتا برای انجام آزمون تحلیل کوواریانس آماده شده است. از طریق مسیر زیر در نرم افزار SPSS آزمون ANCOVA را انجام می دهیم.

Analyze / General Linear Model / Univariate

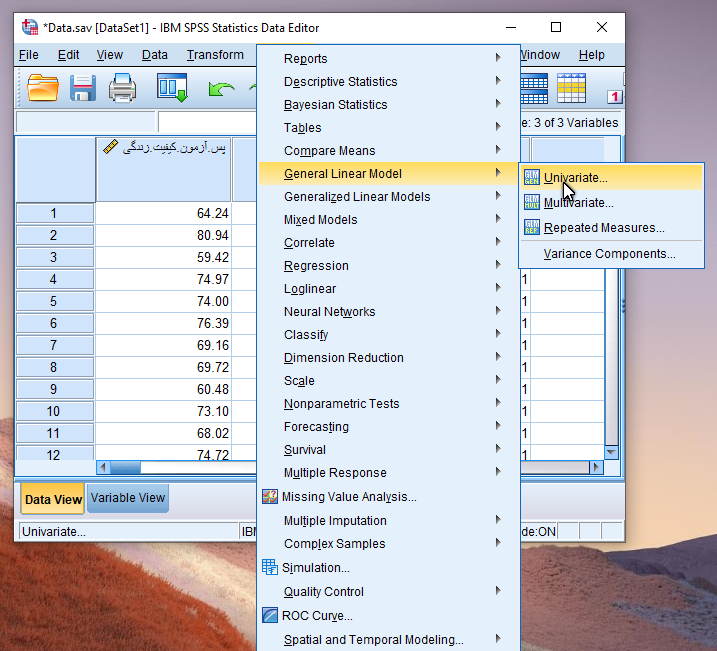
پس از انجام مسیر فوق پنجره زیر جهت تنظیمات تحلیل کوواریانس قابل مشاهده است.

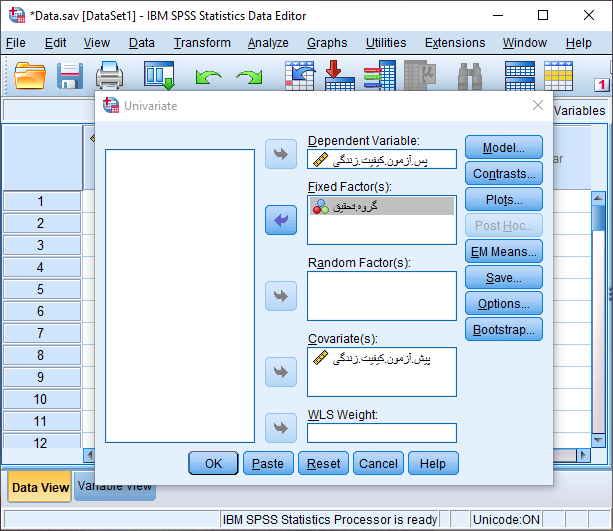
همانند شکل فوق، متغیر کیفیت زندگی پس از مداخله (پس آزمون) را به عنوان متغیر وابسته در کادر Dependent Variable، متغیر کیفیت زندگی قبل از مداخله (پیش آزمون) را به عنوان متغیر کووریت (مخدوش کننده) در کادر Covariate(s) و متغیر گروه را در کادر Fixed Factor(s) به عنوان متغیر مستقل وارد می کنیم. ابتدا برای بررسی پیش فرض همگنی شیب رگرسیونی از طریق دکمه Moldel پنجره زیر را باز می کنیم.

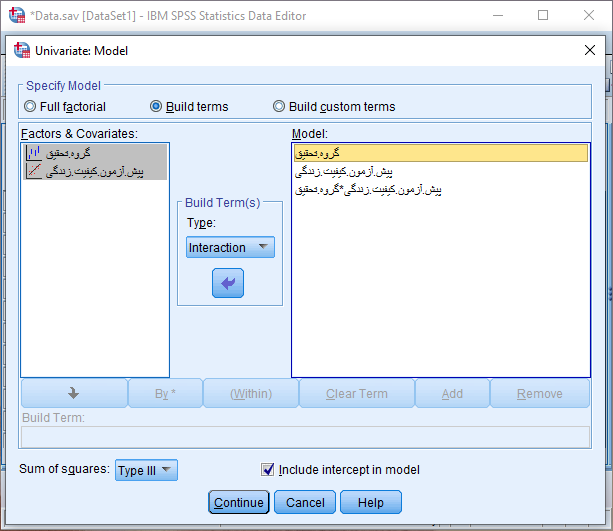
مانند شکل فوق ابتدا در کادر Specify Model گزینه Build terms را فعال می‌کنیم. سپس در کادر Model متغیرهای (گروه تحقیق، پیش آزمون و متغیر ضربی پیش آزمون کیفیت زندگی * گروه تحقیق را وارد می کنیم. با کلیک بر روی دکمه Continue مجدد وارد پنجره قبلی می شویم. حال با کلیک بر روی دکمه OK خروجی نرم افزار به صورت زیر مشاهده می شود.

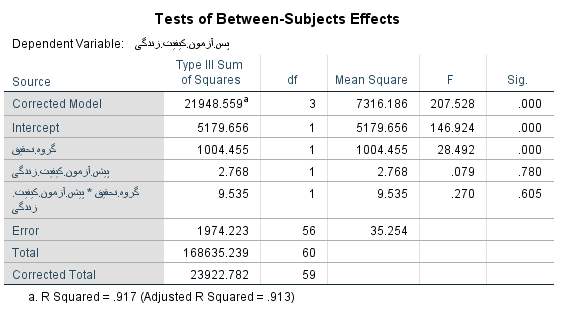
با توجه به جدول فوق ملاحظه می شود سطح معنی داری متغیر گروه تحقیق*پیش آزمون کیفیت زندگی برابر 0.605 و بیشتر از 0.05 می باشد. این امر نشان دهنده این است که پیش فرض همگنی شیب رگرسیون رعایت می شود.

حال برای بررسی پیش فرض همگنی واریانس ها از طریق دکمه Moldel پنجره زیر را باز کرده و مانند شکل زیر تنظیمات لازمه را انجام می دهیم.

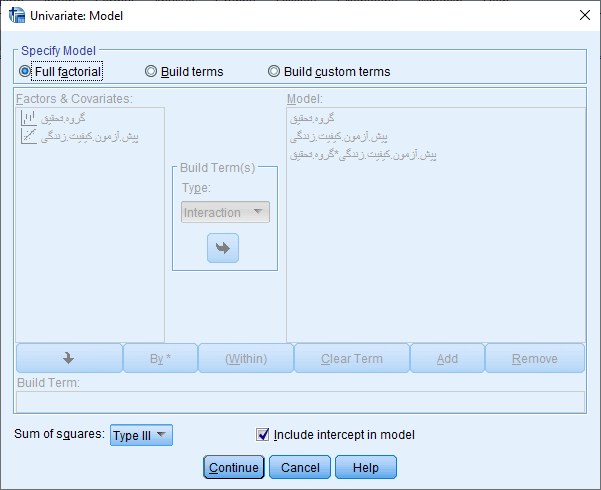
مانند شکل فوق ابتدا در کادر Specify Model گزینه Full factorial را فعال می‌کنیم. با کلیک بر روی دکمه Continue مجدد وارد پنجره قبلی می شویم.

در این پنجره از طریق گزینه Options پنجره زیر باز می شود.

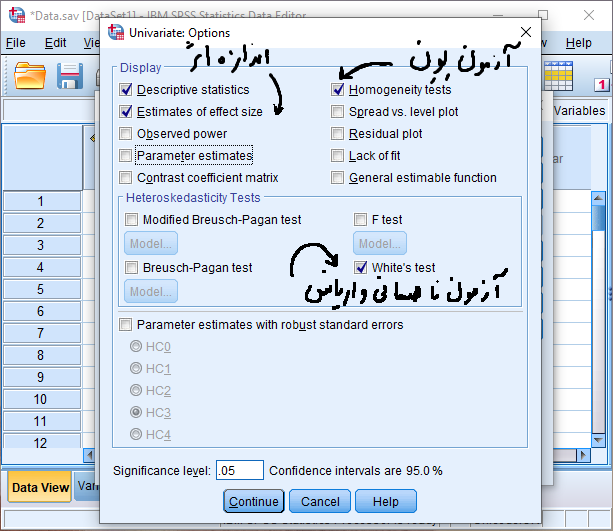
پس از انجام تنظیمات فوق با کلیک بر روی دکمه Continue مجدد وارد پنجره قبلی می شویم. حال با کلیک بر روی دکمه OK خروجی نرم افزار به صورت زیر مشاهده می شود.

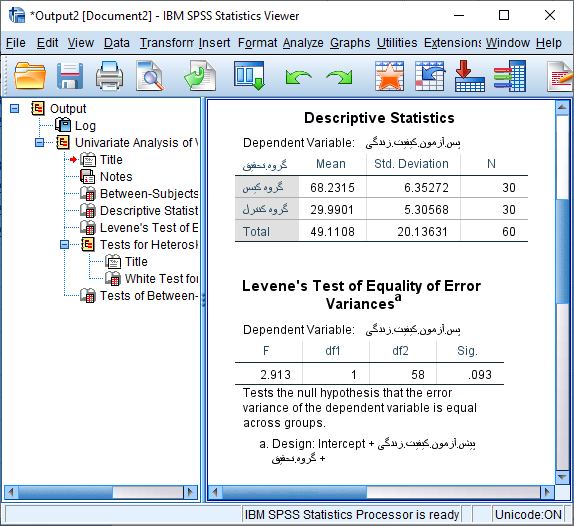
با توجه به سطح معنی ­داری شکل فوق (0.093) فرضیه صفر مبنی بر همگونی واریانس ­ها در دو گروه شاهد و آزمایش در سطح 5 درصد رد نمی­ گردد. در نتیجه فرضیه برابری واریانس ­ها تایید می ­شود.

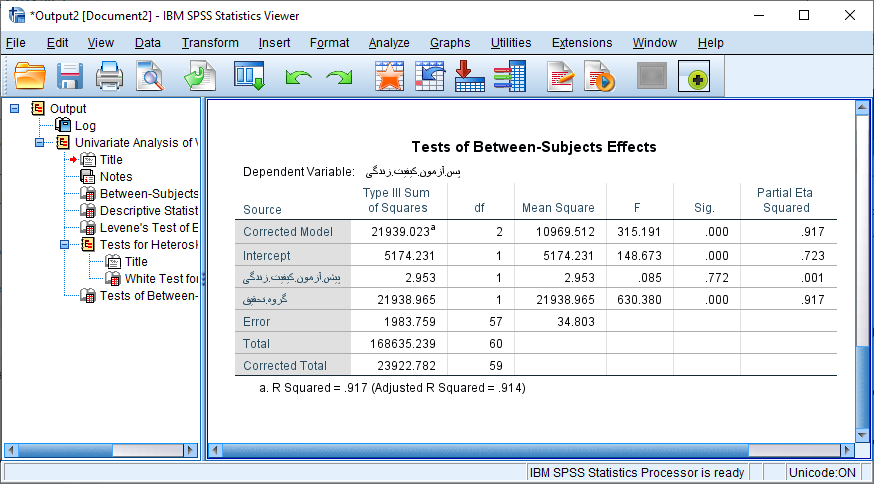
در جدول فوق فوق ملاحظه می­ شود، در پس آزمون نمرات کیفیت زندگی کل آزمایش (گروهی که پیگیری تلفنی دریافت کردند) با نمرات کیفیت زندگی در گروه گواه تفاوت معنی داری وجود دارد (سطح معنی داری کمتر از 0.05). در نتیجه می­ توان دریافت که بیمارانی که مداخله دریافت می­ کنند، نسبت به دیگر افراد، کیفیت زندگی کل بیشتری دارند. به طور کلی مشاهدات بیان می­ کند که پیگیری تلفنی بر بهبود کیفیت زندگی افراد با اندازه اثر (0.917) تاثیر گذار است.

 

منبع: https://cochrana.ir

سایتهایی دارای مقالات علمی فارسی و پژوهشی جهت یافتن موضوع پایان نامه

بهترین سایتهایی که حاوی مقالات علمی فارسی می باشد به صورت گذرا در ذیل به حضور عزیزان بخصوص دوستانی که در کلاس سوال می فرمودند معرفی می شود. یاد آوری می شود این سایتها جزئی از سایتهایی است که دارای مقالات علمی است نه کل آنها. برای دریافت مقالات علمی از اینترنت گذشته از این سایتها شما می توانید با جستجوی حرفه ای در گوگل به مقالات علمی بیشتری دست پیدا کنید البته چون بزرگترین کشور فارسی زبان ایران است طبیعتا این سایتها نیز سایتهای ایرانی خواهد بود. درضمن باید به خاطر داشته باشیم که هنوز تحقیق کاملا علمی تنها از اینترنت بدون مراجعه به کتابخانه و منابع دیگر در کشورهای جهان سوم به دلیل عدم غنای کامل اینترنت میسّر نیست و مقالات علمی اینترنتی در حدّ راهنما و گرفتن ایده و به صورت یک منبع خوب و کاربردی کمکی باید استفاده شود نه به عنوان منبع اولیه و کامل که ما را از منابع دیگر بی نیاز نماید.

اگر خواهان مقالات علمی به زبان انگلسی باشید هرچه بخواهید به دست خواهید آور. فقط کافی است به آدرس

http://www.google.com/schhp?hl=en بروید و موضوع مورد نظر تانرا جستجو نمایید تا مقاله مورد نظر تان را به زبان انگلسی پیدا کنید.

 

سرویس ویژه گوگل برای محققین و جویندگان مقالات علمی

 به زبان فارسی

 

اگر بخواهید به عنوان یک محقق فارسی زبان به مقالات معتبر علمی به زبان فارسی دست پیدا کنید از این صفحه گوگل به این آدرس  _{http://scholar.google.com/advanced_scholar_search?hl=fa}   استفاده فرمایید.در مورد شیوه ای جستجوی حرفه ای در گوگل برای پیدا کردن مقالات علمی یا هر موضوعی که بخواهید انشاء الله در یاد داشتی دیگری قرار فرصت خدمت دوستان خواهیم بود. اینک معرفی چند منبع علمی جامع با شرح مختصری که از سوی خودشان ارائه شده است:

 

بهترین سایتهای فارسی دارای مقالات علمی و تحقیقاتی

 

بانک اطلاعات نشریات ایران

http://www.magiran.com/

در میان سایتهای فارسی زبان بزرگتر و جامعتر از این سایت برای جستجوی مقالات علمی و تحقیقاتی نمی توان یافت. بزرگترین مرجع و نمایشگاه دائمی مطبوعات کشوردر ایران نشریات متعددی به چاپ می رسند که عموما به دلایل مختلف برای مخاطبین شناخته شده نیستند و حتی متخصصین آن رشته نیز از انتشار آنها بی اطلاع می باشند. همچنین بسیاری از علاقمندان و پژوهشگران نیازمند جستجو و مطالعه مقالات و مطالب علمی مندرج در شماره های مختلف نشریات هستند که پاسخ آنها جز با استفاده از فن آوری اطلاعات مقدور نیست..

در این راستا فعالیت سایت از سال ۱۳۸۰ آغاز گردید و ضمن مکاتبه و رایزنی های مکرر با مدیران نشریات، تا کنون موفق به پوشش و ارایه خدمات به بیش از ۱۵۰۰ نشریه در حال انتشار شده ایم. این خدمات شامل درج شناسنامه نشریه، طرح روی جلد و فهرست مطالب هر شماره و اقلام مقاله شناختی آنها با استفاده از مندرجات نشریه می‌باشد. این خدمات فقط با ارسال یک نسخه از هر شماره به نشریات ارایه می شود و کاربران می توانند با استفاده از فهرست الفبایی، فهرست موضوعی و جستجو به نشریات مورد نظر خود دست یابند.

همچنین نشریات می‌توانند متن کامل و یا گزیده مقالات خود را در این سایت در دسترس کاربران ساکن در داخل و خارج کشور قرار دهند.

پژوهشکده اطلاعات و مدارک علمی ایران

http://www.irandoc.ac.ir/

برای اینکه بدانید این سایت تاچه میزان شمارا در تحقیق و کارهای علمی یاری می کند به برخی امکانات آن توجه نمایید: 

-شامل بیش از ۶۰۰۰۰۰ رکورد اطلاعات علمی کشور:

-پایان‌نامه‌های‌ ایران‌ – دکترا و کارشناسی‌ ارشد

-پایان‌نامه‌های‌ فارغ‌التحصیلان‌ ایرانی‌ خارج‌ از کشور

-طرح‌های‌ پژوهشی‌ کشور

-مقالات‌سمینارها،کنگره‌ها و سمپوزیوم‌های‌علمی‌وفرهنگی‌ ایران‌

-مقالات‌ علمی‌ و فنی‌

-گزارش‌های‌ دولتی‌ ایران‌

-فهرستگان‌ نشریات‌ ادواری‌ لاتین‌ موجود در کتابخانه‌های‌ ایران‌

-علوم‌ تربیتی‌

-اطلاعات‌ محققین‌ و متخصصین‌ ارشد کشور

-اطلاعات‌ آب‌

-اطلاعات‌ خزر

 

پایگاه بزرگ علمی SID - جهاد دانشگاهی

http://www.sid.ir/

 

این سایت نیز از غولهای علمی اینترنت به زبان فارسی به شمار می رود. در عصر اطلاعات و جهانی که هرگونه توسعه منوط به دستیابی مستمر و علمی به اطلاعات است، ساماندهی و پردازش اطلاعات و مقالات علمی منتشر شده در نشریات علمی –پژوهشی اهمیتی خاص یافته است. بر این اساس جهاد دانشگاهی در تاریخ ۱۶ مرداد ۱۳۸۳ اقدام به افتتاح ” مرکز اطلاعات علمی جهاد دانشگاهی ” نمود. اهداف تاسیس مرکز اطلاعات علمی جهاد دانشگاهی آنچنان که در اساسنامه آن آمده است ” ترویج و اشاعه اطلاعات علمی ، گسترش و ارتقاء خدمات اطلاع رسانی به محققان ، سرعت بخشیدن به کاوش های علمی و افزیش اثر بخشی تحقیقات در کشور است." مرکز اطلاعات علمی جهاد دانشگاهی تحت نظارت شورای علمی ، خدمات خود را از طریق پایگاه اینترنتی http://www.sid.ir/ به عنوان بانک اطلاعات علمی کشور و در آینده نزدیک در سطح منطقه ارائه می دهد و تلاش نموده از تجربه های مشابه در داخل و خارج از کشور جهت بهبود ، روزآمدی و جامعیت اطلاعات استفاده کند.

خدمات عمده پایگاه SID عبارتند از :

- جستجو و ارائه چکیده مقالات نشریات علمی – پژوهشی کشور

- دسترسی به متن کامل (Full Text) مقالات

- معرفی و ارائه مقالات نشریات ایرانی نمایه شده در ISI

- دسترسی به مجموعه مقالات محققان ایرانی چاپ شده در نشریات بین المللی

- سرویس گزارش های استنادی نشریات علمی – پژوهشی کشور (JCR)

از طریق شاخص تاثیر (Impact Factor) و شاخص آنی (Immediacy Index)

- معرفی نشریات و نویسندگان مقالات پر استناد

- سرویس ارسال الکترونیکی مقالات (Online Submission) و رهگیری پیشرفت کار توسط نویسندگان.

این بود معرفی مختصر چند سایت مفید و معتبر علمی که حاوی مقالات و مطالب ارزنده علمی و گنجینه بزرگ ازمقالات گوناگون علمی می باشد. سایت ویکی پیدیا نیز به عنوان یک دائرة‌ المعارف عمومی دارای برخی مقالات خوب علمی نیز می باشد.

همانگونه که قول داده بودم اگر فرصت دست داد مطلبی در مورد نحوه ای جستجوی حرفه ای مقالات و مطالب مورد نظر خویش در گوگل نیز نشر خواهم نمود.

برخی سایتهای مفید دیگر برای تحقیقات علمی به زبان فارسی

راستی یادم رفت بگویم:سایت کتابخانه ملی ایران، پایگاه اطلاع رسانی کتابخانه های ایران، خانه کتاب ایران  از سایتهایی است که می تواند به عنوان منابع مفیدی برای محققان و پژوهشگران در جهت آشنایی با منابع و کتابهای فارسی و غیر فارسی می باشد. گرچند در این سایتها متن کتابها و مقالات قابل دسترسی نیست اما برای پیدا کردن منبع و سرنخ در زمینه موضوع مورد نظر محققین بهترین گزینه است و یک شبه کار صد ساله را انجام می دهد.

 

مترجم گوگل در خدمت پژوهشگران علمی

 

سرویس ترجمه گوگل شاهکار دیگر گوگل عزیز برای محققان و جویندگان مطالب علمی به زبانهای غیر مادری شان است. این سرویس از اکثر زبانهای زنده دنیا بخصوص زبان فارسی به خوبی پشتیبانی می کند و واقعا دستیار ماهر و کارگشا برای محققان به حساب می آید.

برای استفاده از سرویس ترجمه گوگل به این صفحه با این درس:  http://translate.google.com/#en|fa|   بروید و درچوکات سمت چپ متن مورد نظر را کپی کرده از بالا گزینه   را بفشارید تا متن شما را به فارسی ترجمه کند. برای تعویض زبان این سرویس می توانید از گزینه های تعویض زبان که در قسمت بالای صفحه جا سازی شده است استفاده نمایید.

رسم نمودار در SPSS

نمودارهای خطی (line charts):

در نمودارهای خطی شاخص آماری به شکل خط در سطوح متغیرهای طبقه ای ارائه می شود.گاهی داده ها به جای اینکه کمیت پیوسته باشند مانند وزن، شمارشی هستند مانند تعداد دندانهای خراب، تعداد فرزندان، تعداد حوادث رانندگی در روز، میزان بارندگی سالهای مختلف. اگر تعداد مقادیر متمایز زیاد نباشد برای ساختن توزیع فراوانی به جای انکه رده‎ها را فواصل منظم در نظر بگیریم هر مقدار به عنوان یک رده به کار می‎رود.

مزایای نمودار خطی:

در این است که می توان اثرات تعاملی متغیرهای طبقه ای را بر روی متغیرهای وابسته مشاهده کرد و برای متغییر های کمی مناسب است.

نمودارهای خطی فراوانی نسبی:

مقادیر متمایز به صورت نقاط روی محور افقی مشخص شده و سپس از نقاط حاصل، خط هایی عمود بر محور رسم می شود به طوریکه ارتفاع هر یک برابر با فراوانی نسبی مقدار مربوطه باشد.

در این حالت، خطوط جایگزین مستطیل ها می شوند تا بر این موضوع تاکید شود که فراوانی ها واقعا روی فاصله پخش نشده اند.

نکته رسم نمودار خطی در SPSS :

برای اطمینان از صحت و درستی نرمال بودن توزیع فراوانی باید در خروجی spss مقادیر پارامترهای skewenss (چولگی) و kurtosis (کشتاوری) را بررسی کنید:

• اگر مقدار kurtosis یک عدد مثبت باشد، داده ها دارای یک توزیع نرمال با ارتفاع بالا هستند.
• اگر مقدار kurtosis یک عدد منفی باشد، داده ها را یک توزیع نرمال با ارتفاع پایین هستند.
• اگر مقادیر kurtosis و skewenss اختلاف زیادی از عدد ۵ داشته باشند، داده ها دارای توزیع نرمال نیستند

رسم نمودار خطی در spss:

  graphs/Legacy dialogs سپس line و روی کادر باز شده line charts باز می شود این نمودار به سه شکل زیر می باشد:

۱- نمودار ساده Simple

۲- نمودار چند گانه Multiple : برای نمایش توزیع دو متغییر نسبت به هم استفاده می شود.

۳- نمودار تکه خطی drop-line : که کمیه و بیشینه دو متغییر نسبت به هم نمایش می دهد.

۴- یکی از سه حالت فوق انتخاب کرده سپس define کلیک کرده و کادر مربوط به آن باز می شود

برای مثال : تعداد فرزندان در هر خانوار را ثبت نموده ایم و نمودار خطی حاصل از آن را ترسیم می نماییم.

Graphs> chart builder > ok

و در بخش نمودارها Line را انتخاب می نماییم. و متغیر مورد نظر را کشیده و به بخش پایین می بریم.

 

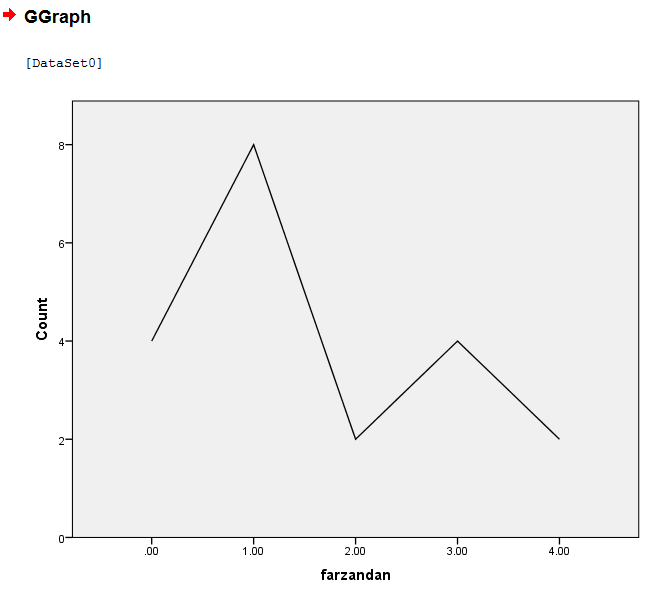
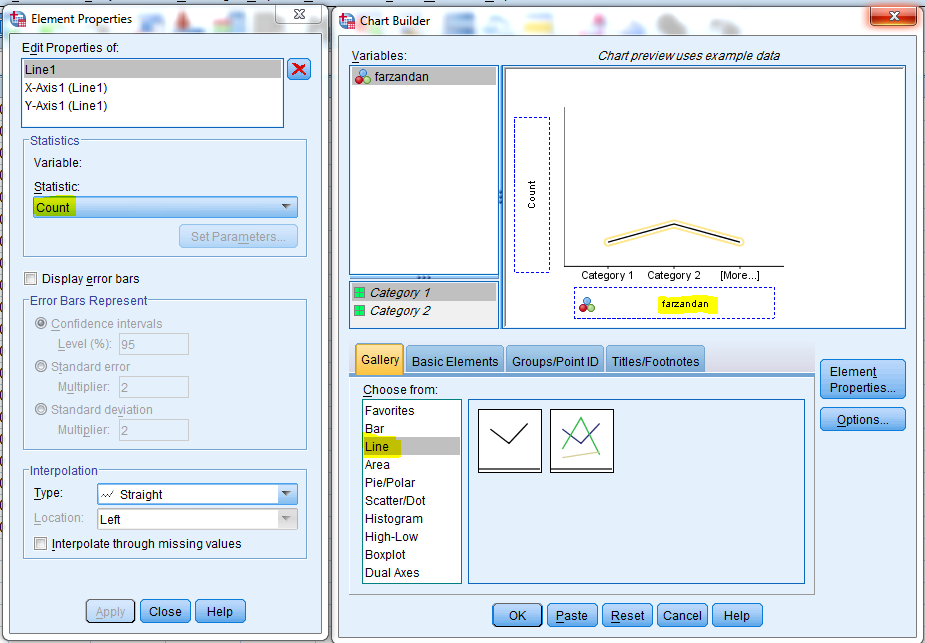OK کرده و نمودار حاصل بدست میاد. در جدول سمت چپ Statistics گزینه های مختلف را میتوان انتخاب کرد. Count فراوانی را در نمودار ترسیم میکند و Percentage فراوانی نسبی را در نمودار می دهد. بعد از انتخاب گزینه مد نظر در statistic باید گزینه Apply را کلیک کرد.

     نمونه 

نمونه مثال:

منوی Analyze زیر منوی General Linear Model و زیرمنوی Repeated Measures چنین نموداری وجود دارد.

                                                                  

 

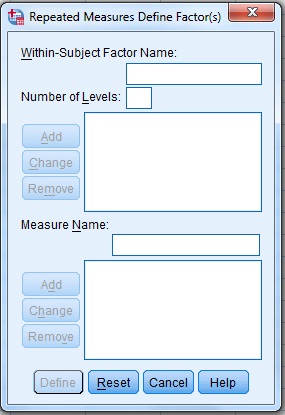
مثلا شما از یک متغیر کمی چندحالته (مثل سطح تحصیلات) ۲ الی ۲۹ نمونه دارید و میخواهید روند آنها را با نمودار خطی در spss محاسبه کنید، بنابراین مسیر بالا را طی کرده و در جعبه گفتگوی نمایان شده، تعداد نمونه ها را وارد کرده و Add و Define کنید.

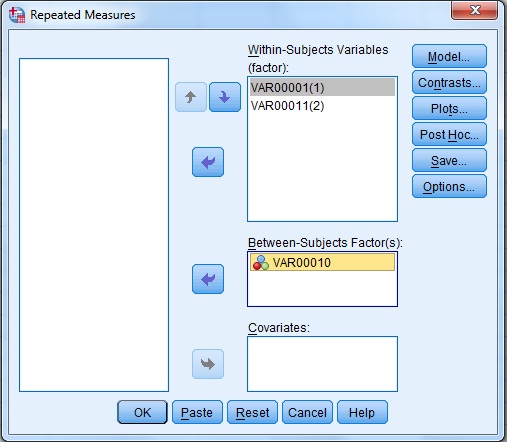
پس از آن همۀ نمونه ها را به بخش  Within subject variables و متغیر کیفی را به بخش Between subject variables انتقال داده و جعبه گفتگوی Plots را انتخاب کنید.

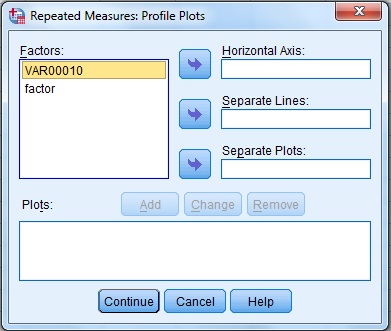
در مرحله باید متغیر Factor1 را به Separate Lines و متغیر کیفی را به Horizontal Axis منتقل کرده، Add و Continue نمایید. درنهایت Ok کنید.

نمودارهای تعاملی:

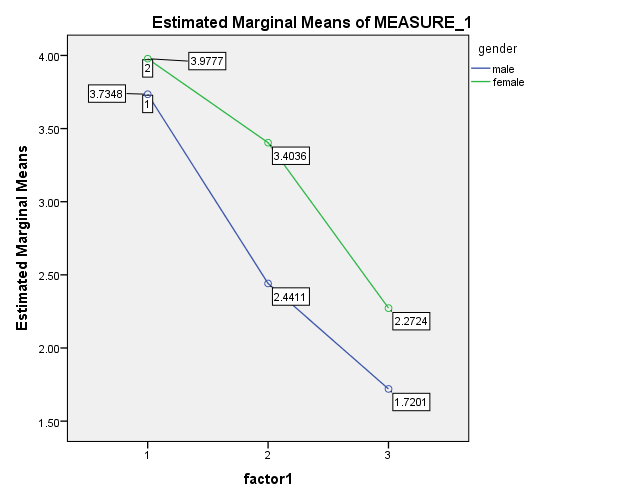
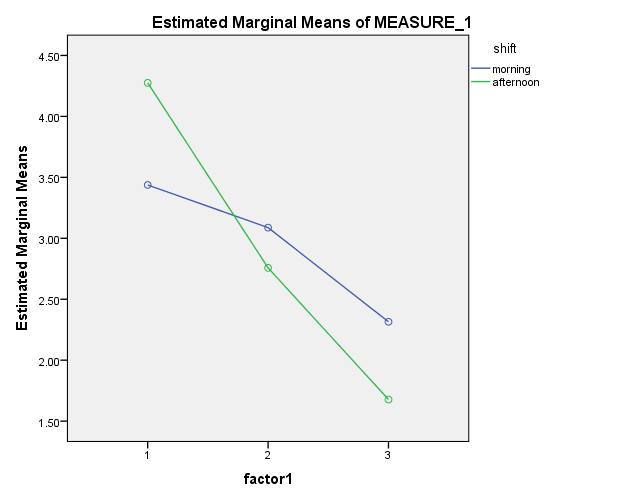
برای ساخت نمودارهای تعاملی کافی است به جای فعال نمودن گزینه ی Simple از گزینه ی Multiple استفاده شود و جهت بررسی اثرات تعاملی متغیرهای مستقل، باید دو متغیر مستقل را به دلخواه یک در جعبه ی Category Axisو دیگری را در جعبه ی Define line by قرارد هید.

تحلیل عاملی تاییدی در نرم افزار اموس (AMOS) و (LISREL)

تحلیل عاملی تاییدی اساسا یک روش آزمون فرضیه است و زمانی استفاده می شود که محقق ارتباطات شاخص ها (عوامل) با سوالات (گویه ها) را فرضیه سازی کرده و می خواهد داده ها را برای ساختار از قبل تعیین شده بسنجد. بدین صورت که مجموعه گویه های هر عامل یا شاخص (factor)، منحصرا بعد مربوط به خود را اندازه گیری می کنند.

کاربرد تحلیل عاملی تاییدی

تحلیل عاملی تاییدی این مطلب را که آیا گویه هایی (indicators) که برای معرفی هر بعد ارائه شده اند؛ واقعا معرف آن هستند یا نه، می آزماید و گزارش می دهد که گویه های انتخابی با چه دقتی معرف یا برازده عامل یا متغیر پنهان (latent variables) خود هستند.

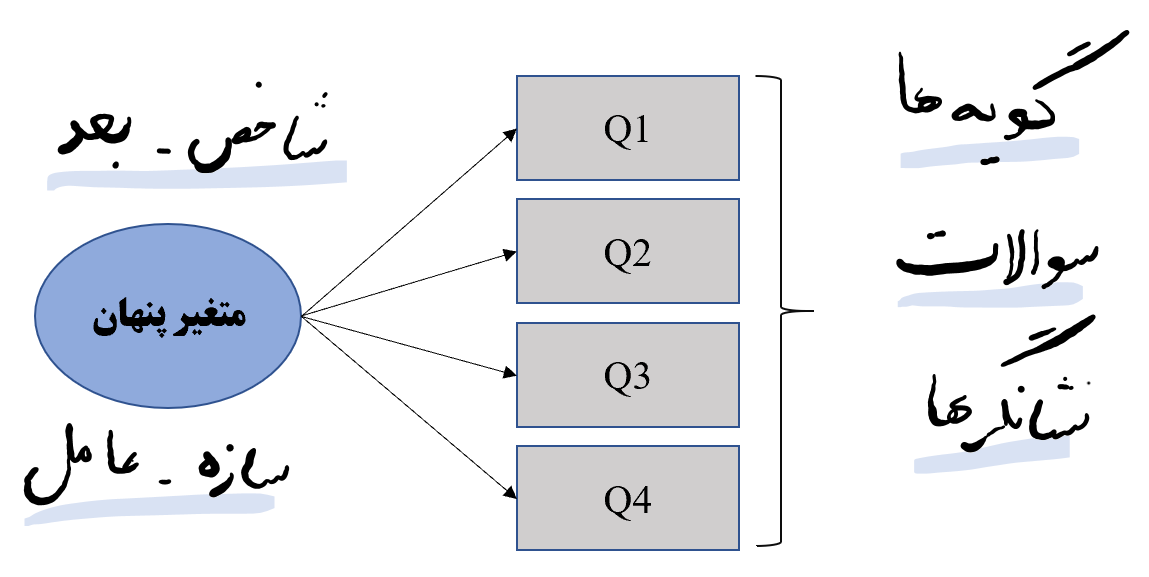
در شکل فوق نمایی از مدل ساده ای از تحلیل عاملی تاییدی نشان داده شده است که در آن دایره ها نشان دهنده متغیرهای پنهان و مربع ها نشان دهنده متغیرهای آشکار هستند.

مراحل انجام تحلیل عاملی تاییدی

اولین مرحله در انجام تحلیل عاملی رسم مدل اندازده گیری در نرم افزار می باشد. پس از رسم مدل و برازش آن، بررسی بارهای عاملی و حذف گویه هایی که بار عاملی کمی دارند در مرحله دوم قرار می گیرد. در مرحله سوم، نوبت به بررسی شاخص های برازش مدل می باشد.

1-رسم مدل اندازه گیری برای تحلیل عاملی تاییدی

شکل زیر (مدل دارای دو عامل می باشد) اجزای تشکیل دهنده مدل اندازه گیری برای انجام تحلیل عاملی تاییدی در اکثر نرم افزارهای معادلات ساختاری را نشان می دهد. همانطوری که در شکل مشخص است، فلش دو طرفه بین عوامل، نشان دهنده همبستگی بین متغیرهای پنهان، اعداد روی پیکان های یک طرفه از متغیرهای پنهان به سمت متغیرهای آشکار نشان دهنده بارهای عاملی می باشند. همچنین مقدار واریانس خطا و مقدار کوواریانس بین خطاها نیز در شکل نشان داده شده است.

2-بررسی بارهای عاملی در تحلیل عاملی تاییدی (CFA)

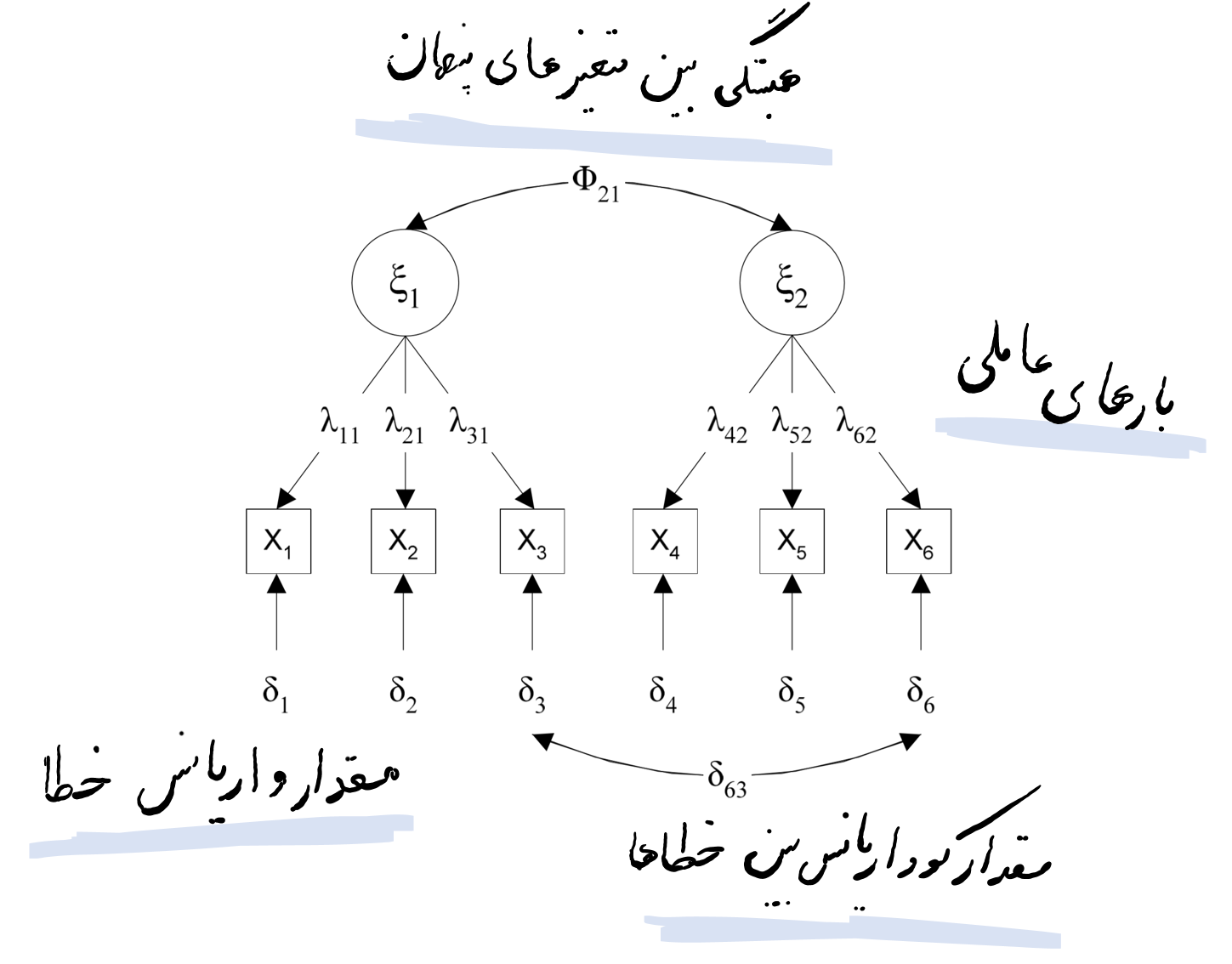
بارهای عاملی از طریق محاسبه مقدار ارتباط گویه های یک سازه با آن سازه محاسبه می‌شوند که اگر این مقدار برابر و یا بیشتر از مقدار 0.4 شود، مؤید این مطلب است که واریانس بین سازه و شاخص‌های آن از واریانس خطای اندازه‌گیری آن سازه بیشتر بوده و پایایی در مورد آن مدل اندازه‌گیری قابل قبول است. نکته مهم در اینجا این است که اگر محقق پس از محاسبه بارهای عاملی بین سازه و گویه های آن با مقادیری کمتر از 0.4 مواجه شد، باید آن گویه ها (سؤالات پرسش ‌نامه) را اصلاح نموده و یا از مدل تحقیق خود حذف نماید.

3-شاخص های اندازه گیری تحلیل عاملی تاییدی

پس از برازش مدل ابتدا نیاز است بررسی شود آیا مدل مورد بررسی کفایت لازم برای بررسی روابط (یعنی معنی داری ضرایب مسیر و جملات خطا) را دارد یا خیر. برای این منظور، از شاخص های نیکویی برازش استفاده می­ کنند، پژوهشگران جهت ارزیابی نیکویی برازش از سه گروه شاخص ­ها شامل شاخص­ های برازش مطلق، شاخص ­های برازش تطبیقی، شاخص ­های برازش مقتصد جهت حصول اطمینان از مدل نظری پژوهش استفاده می ­کنند.

شاخص ­های برازش مطلق

شاخص ­های برازش مطلق شاخص­ هایی هستند که بر مبنای تفاوت واریانس ­ها و کوواریانس ­های مشاهده شده از یک طرف و واریانس ­ها و کواریانس­ های برآورد شده بر مبنای پارامترهای مدل تدوین شده از طرف دیگر قرار دارند و با نزدیک شدن این مقادیر به یکدیگر این شاخص­ ها بهبود خواهند یافت. شاخص نیکویی برازش (GFI)، شاخص نیکویی برازش اصلاح شده (AGFI)، نسبت مجذور خی­ دو به درجه ­ی آزادی از این قبیل شاخص­ ها می ­باشند.

شاخص ­های برازش تطبیقی

شاخص­ های تطبیقی در واقع گامی در جهت تکمیل شاخص ­های برازش مطلق محسوب می­ شوند. به این ترتیب که با مبنا قراردادن یک یا چند مدل، مدل نظری تدوین شده تحت آزمون را با آن مقایسه و نشان می ­دهد که آیا به لحاظ آماری قابل قبول­تر تلقی می­ شود، ضعیف ­تر است و یا اینکه تفاوتی با آن ندارد.

شاخص ­های برازش مقتصد

شاخص­ های برازش مقتصد، شاخص ­هایی هستند که به وسیله آن ­ها سعی می­ شود تا مهمترین نقطه ضعف شاخص­ های برازش مطلق یعنی بهبود مقدار شاخص برازش با افزایش پارامتر به مدل جبران شود. مبنای اصلی در این گروه از شاخص ­های برازش آن است که به ازای هر پارامتری که به مدل افزوده می­ شود این شاخص ­ها جریمه می­ شوند.

شاخص ­های برازش مانند : شاخص توکر ولیوایس (TLI)، شاخص برازش این­کری­منتال (IFI)، شاخص تطبیقی برازش (CFI) و ریشه ­ی میانگین مجذور برآورد خطای تقریب (RMSEA)، کمتر تحت تاثیر عوامل مزاحم و بیرونی قرار می­ گیرند و نتیجه به­ دست آمده بیشتر مبین نقص در برازش مدل است؛ یعنی اگر یعنی، اگر در تحلیل برازش مناسبی وجود ندارد، به علت ماهیت مدل آن است و کمتر تحت تأثیر عوامل مزاحم و بیرونی است.

تحلیل عاملی تاییدی در نرم افزار لیزرل (Lisrel)

برای انجام تحلیل عاملی تاییدی در نرم افزار لیزرل فرض می کنیم پرسشنامه ای در دست محقق است که دارای سه بعد می باشد. ابتدا شاخص های پرسشنامه مورد نظر را در نرم افزار به صورت زیر رسم کرده و مدل را اجرا می کنیم :

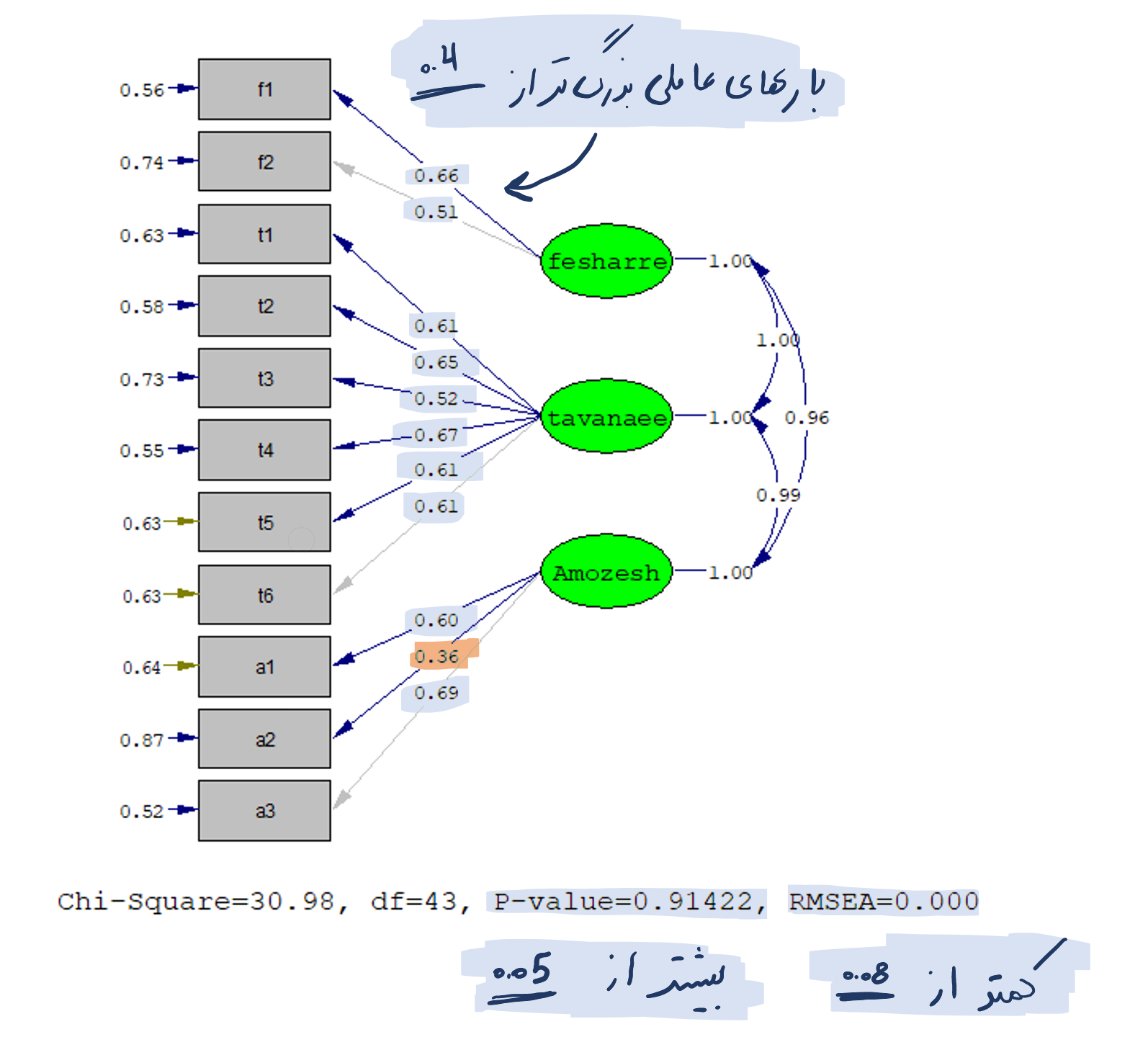
همانطوری که از شکل مشخص است، اکثر بارهای عاملی بدست آمده از برازش مدل بالاتر از 0.4 هستند. در صورتی که تنها بار عاملی گویه a2 برابر 0.36 می باشد که اختلاف چندانی با 0.4 ندارد. حذف این گویه زمانی لازم می شود که شاخص های برازش مدل در حد قابل قبولی نبوده و با حذف این گویه بهبود یابند.

معیارهای نیکویی برازش در نرم افزار لیزرل (Lisrel)

پس از بررسی بارهای عاملی، باید نسبت به برازش مدل مفهومی تحقیق با داده های گردآوری شده نیز اطمینان حاصل نمود. به این منظور، توجه به شاخص های مندرج در زیر مدل و مقایسه آن ها با سطح قابل قبول هر یک از آن ها ضروری است. در نرم افزار معادلات ساختاری لیزرل همیشه چهار شاخص کای اسکوئر (Chi-Square)، درجه آزادی (df)، سطح معنی داری (P-Value) و جذر برآورد واریانس خطای تقریب (RMSEA)، زیر نمودار نشان داده می شود.

مانند جدول زیر اگر نسبت مجذور کای به درجه آزادی کوچکتر از 4 باشد مورد قبول است. مقدار بزرگتر از 0.05 برای سطح معنی داری و مقدار کوچکتر از 0.08 برای جذر برآورد واریانس خطای تقریب نشان دهنده برازش مدل با داده های گردآوری شده است.

شاخص	نماد	مقدار قابل قبول
نسبت کای اسکوئر به درجه آزادی	Chi-Square/df	کوچکتر از 4
سطح معنی داری	P-Value	بزرگتر از 0.05
جذر برآورد واریانس خطای تقریب	RMSEA	کوچکتر از 0.08

مهمترین شاخص های اندازه گیری تحلیل عاملی تاییدی در lisrel

در شکل فوق نیز مهمترین شاخص های اندازه گیری کیفیت تحلیل عاملی تاییدی هایلایت شده است که همگی در بازه قابل قبولی قرار دارند. CFI و NFI، شاخص هایی هستند که برازش مدل پیشنهاد شده به مدل مستقل (که فرض می­کند بین داده­ ها رابطه ­ای وجود ندارد) را می­ سنجد و به ترتیب در مدل برابر 1 و 0.96 هستند. با توجه به این که مقادیر 0.90 و بالاتر قابل قبول می­باشند، این اندازه­ها نیز نمایانگر برازش قابل قبول مدل هستند.

RMSEA، متوسط مانده های بین همبستگی/ کوواریانس مشاهده شده نمونه و مدل مورد انتظار برآورد شده از جامعه است که بنابر توصیه لوهلین مقدار کمتر از 0.08 به معنای برازش خوب می­ باشد. GFI نیز مقدار نسبی واریانس­ ها و کوواریانس­ ها را به گونه مشترک از طریق مدل ارزیابی می ­کند. ویژگی خاص شاخص GFI این است که به حجم نمونه بستگی ندارند. دامنه تغییرات این دو شاخص بین صفر و یک می باشد و مقدار برابر یا بزرگ تر از 0.90 نمایانگر برازش مطلوب است.

تحلیل عاملی تاییدی در نرم افزار اموس (AMOS)

انجام تحلیل عاملی تاییدی در نرم افزار اموس (AMOS) بسیار شبیه به نرم افزار لیزرل می باشد. بدین صورت که ابتدا مدل را مانند قبل رسم کرده و آن را اجرا می کنیم. برای انجام تحلیل عاملی ابتدا بایستی بارهای عاملی و بعد از آن شاخص های نیکویی برازش مدل بررسی شود.

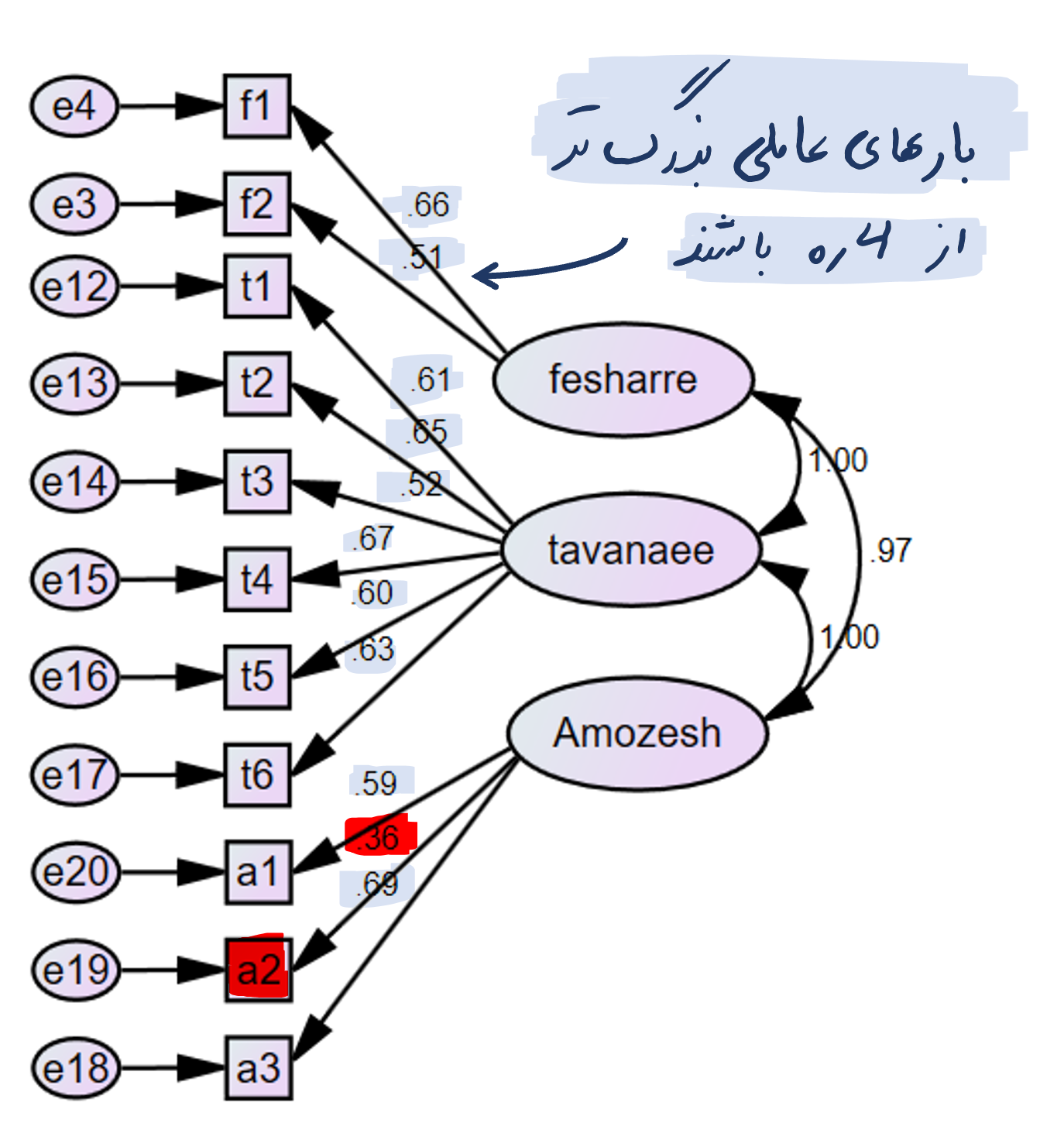
اعداد به دست آمده بر روی فلش ها در شکل فوق، بارهای عاملی برآورد شده را نشان می دهد که بیانگر میزان همبستگی متغیرهای آشکار و پنهان می باشد. فلش های کوچکی که از بیرون به سمت متغیرهای آشکار رسم شده اند، نشان دهنده برآورد میزان خطای مربوط به هر متغیر می باشند. در نمودار فوق که مقادیر استاندارد شده روابط بین متغیرها را نشان می دهد. بارهای عاملی مندرج بر روی فلش ها بیشتر از 0.4 است و بیانگر این است که گویه های مورد نظر، سنجه های خوبی برای متغیر پنهان هستند. در صورتی که گویه ای با بار عاملی کمتر از 0.4 وجود داشته باشد لازم است با احتیاط این موارد را حذف کرده و مجددا تحلیل عاملی تاییدی را تکرار کنیم.

با توجه به شکل فوق ملاحظه می شود بار عاملی گویه a2 برابر 0.36 و کمتر از 0.4 می باشد. حتی الامکان و در صورتی که شاخص های برازش مدل در سطح قابل قبولی باشند از حذف آن صرف نظر می کنیم.

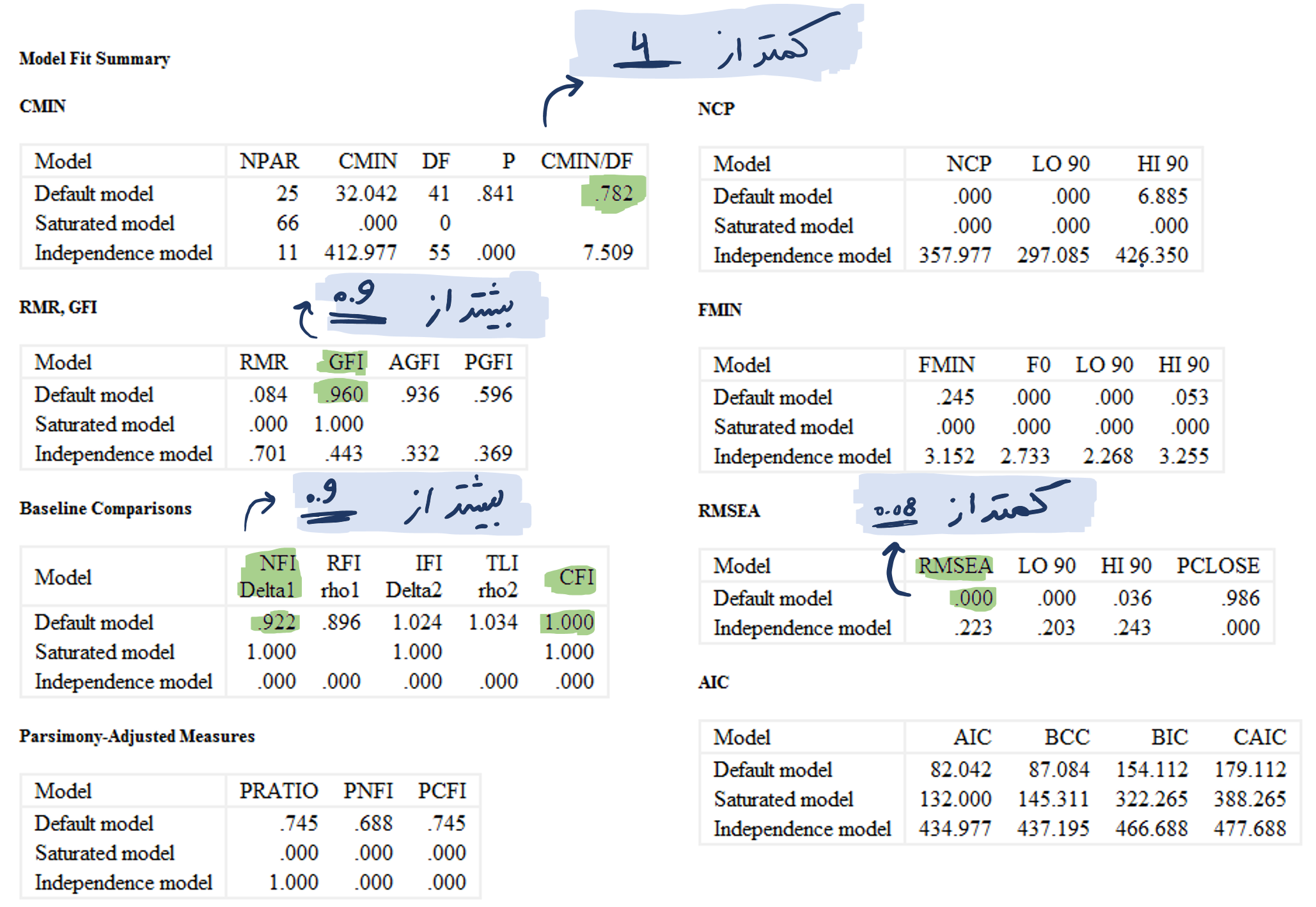
در شکل فوق مهم ترین شاخص های نیکویی برازش مدل برای تحلیل عاملی تاییدی در نرم افزار AMOS هایلایت شده است. با توجه به مقادیر مشاهده شده همه شاخص ها در بازه قابل قبولی قرار گرفته اند.

تحلیل عاملی تاییدی در نرم افزار اسمارت پی ال اس (SmartPLS)

انجام تحلیل عاملی تاییدی در نرم افزار SmartPLS اندکی با نرم افزارهای قبل تفاوت دارد. اولین تفاوت در رسم مدل است. همانطوری که می دانیم در این نرم افزار امکان رسم فلش دو طرفه برای بیان کوواریانس وجود ندارد. مانند شکل زیر برای تحلیل عاملی تاییدی متغیرهای پنهان را به متغیر اصلی خود رسم کرده و تحلیل عاملی تاییدی مرحله دوم را انجام می دهیم.

 

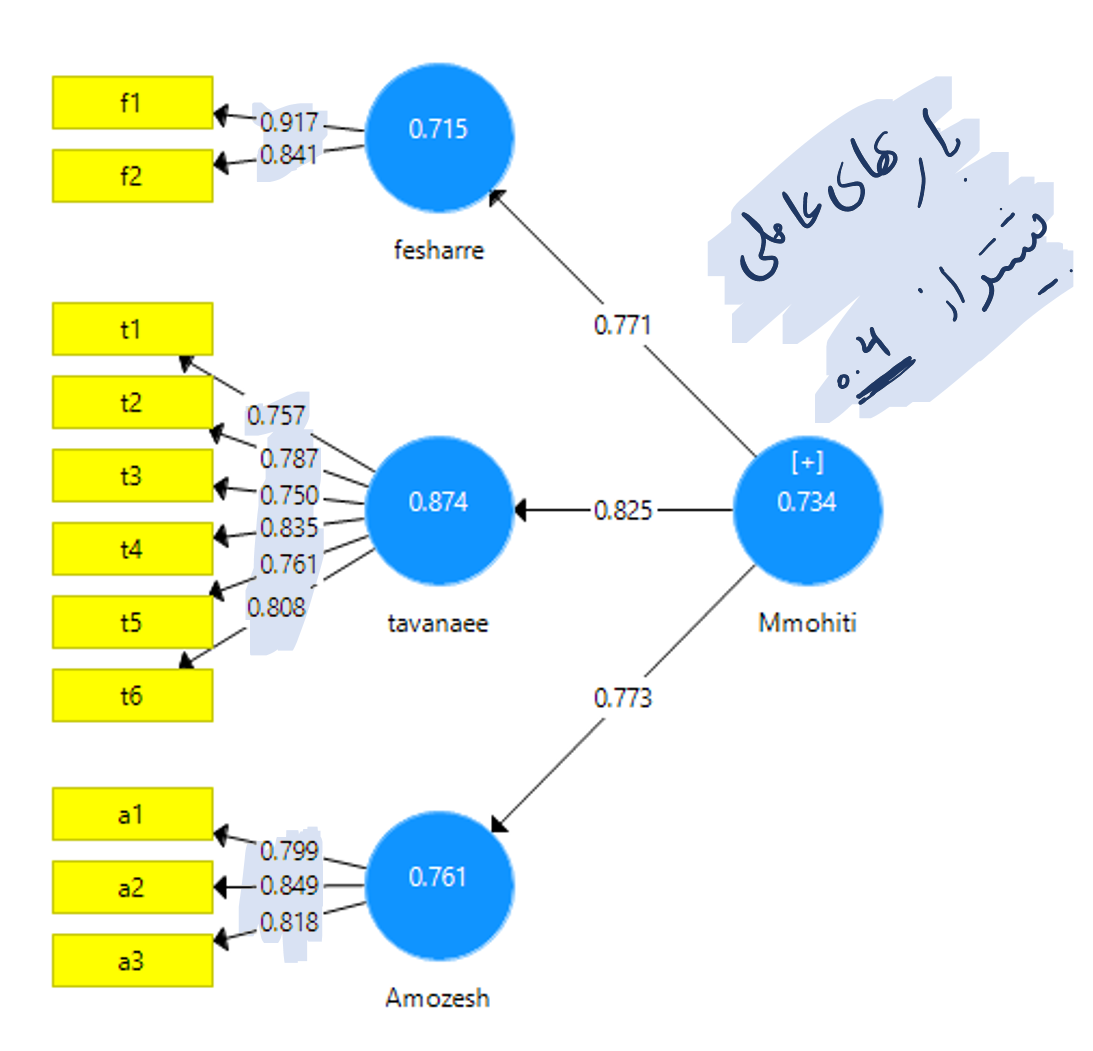
در نرم افزار معادلات ساختاری SmartPLS شاخص های آلفای کرونباخ، ضریب پایایی ترکیبی (CR) و میانگین واریانس استخراجی (AVE) برای تحلیل عاملی تاییدی نیز گزارش می شود. که نتایج آن به شرح زیر است.

 

جدول روایی و پایایی متغیرها در نرم افزار SmartPLS

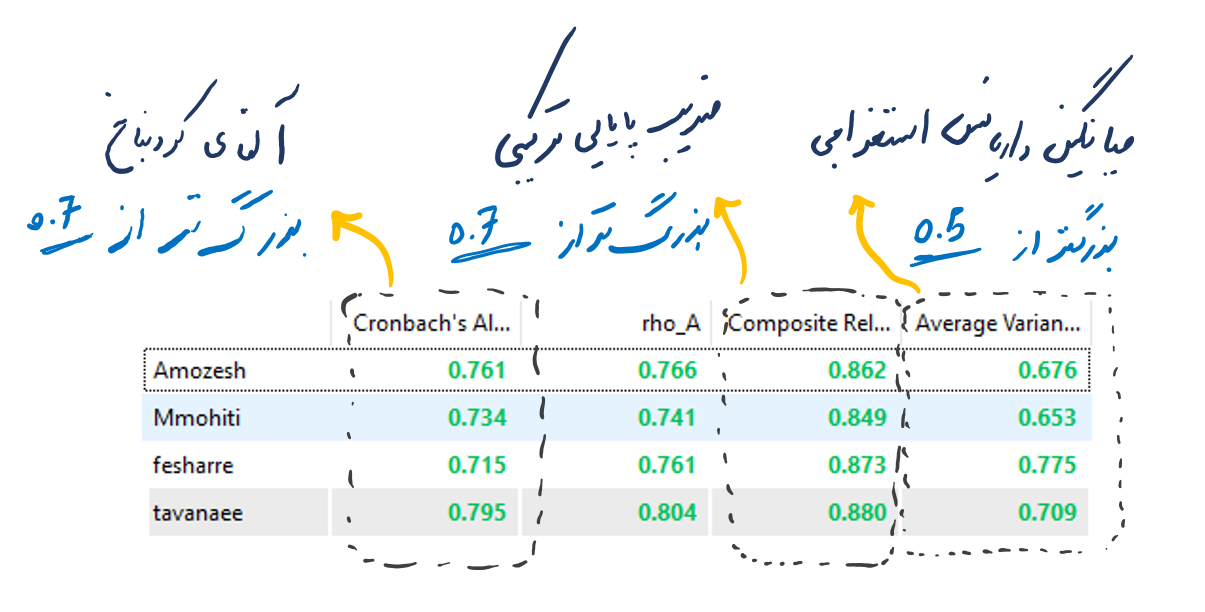
با توجه به اینکه اعداد آلفای کرونباخ، پایایی ترکیبی (سازگاری درونی) و AVE همگی در بازه مربوطه قرار گرفته ­اند، می­ توان مناسب بودن وضعیت پایایی و روایی همگرای مدل پژوهش را تایید کرد.

معیار مهم دیگری که با روایی واگرا مشخص می­ گردد، میزان رابطه ­ی سازه با شاخص ­هایش در مقایسه رابطه آن سازه با سایر سازه­ ها است؛ به ­گونه­ ای که روایی واگرای قابل قبول یک مدل حاکی از آن است که یک سازه در مدل تعامل بیشتری با شاخص­ های خود دارد تا با سازه ­های دیگر. نتایج جدول روایی واگرا به صورت زیر می باشد :

جدول روایی واگرا در نرم افزار SmartPLS

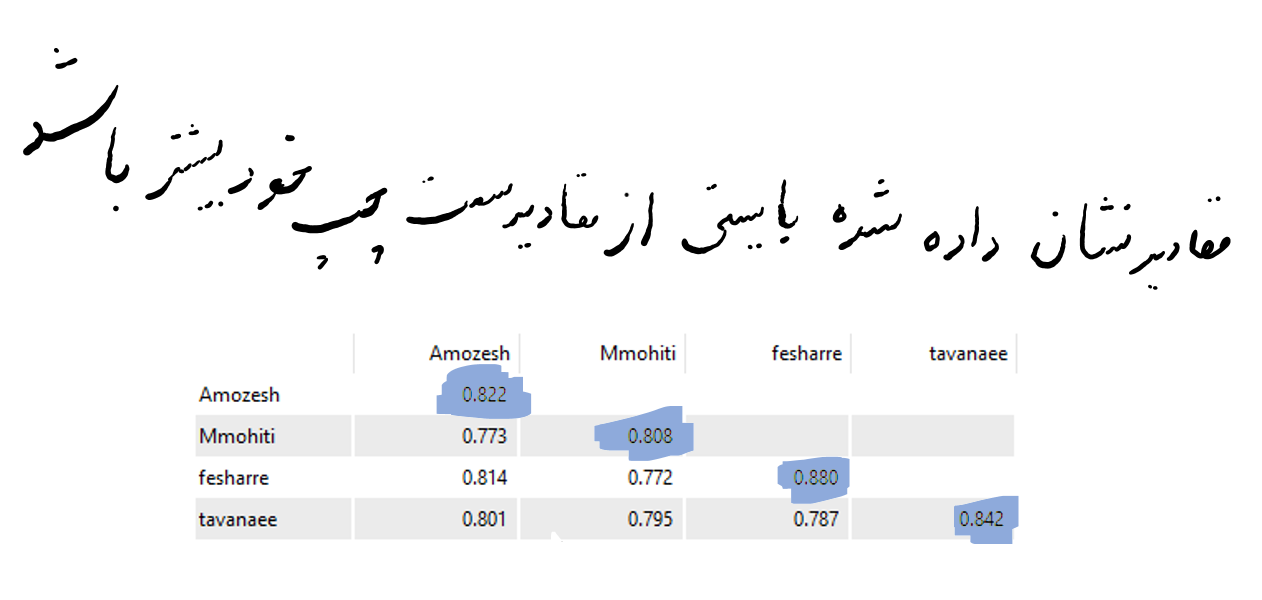
فورنل و لارکر (1981) بیان می کنند : روایی واگرا وقتی در سطح قابل قبول است که میزان AVE برای هر سازه بیشتر از واریانس اشتراکی آن سازه و سازه­ های دیگر (مربع مقدار ضرایب همبستگی بین سازه ­ها) در مدل باشد. بررسی این امر به وسیله یک ماتریس صورت می­ پذیرد که خانه ­های این ماتریس حاوی مقادیر ضرایب همبستگی بین سازه­ ها و جذر مقادیر AVE مربوط به هر سازه است. این مدل در صورتی روایی واگرای قابل قبولی دارد که اعداد مندرج در قطر اصلی از مقادیر زیرین خود بیشتر باشند.

در واقع ماتریس فورنل و لارکر همان ماتریس خروجی از نرم افزار است با این تفاوت که در قطر اصلی مقدار جزر AVE  متغیرها وارد می شود و نکته دیگر اینکه تنها متغیرهای پنهان مرتبه اول در ماتریس فورنل و لارکر وارد می شوند. همان طور که در جدول بالا مشاهده می شود، مقادیر موجود در روی قطر اصلی ماتریس، از کلیه مقادیر موجود در ستون مربوطه بزرگتر است. بنابراین نتیجه می گیریم این مدل از روایی واگرای قابل قبولی برخوردار است.

 

منبع:  https://cochrana.ir
 

متغیر میانجی و تعدیل گر در نرم افزار Smart PLS

در این پست قصد داریم به بررسی مطالب تکمیلی و ذکر نشده در رابطه با نرم افزار smart PLS بپردازیم. امیدواریم که مورد توجه شما علاقه مندان قرار گیرد.

رسم و آزمون متغیر میانجی در اسمارت پی ال اس

به طور خلاصه متغیر میانجی متغیری است که از متغیر مستقل به آن فلش رسم شده و از آن متغیر به متغیر وابسته فلش وارد می شود. رسم متغیر میانجی در نرم افزار SmartPLS تنظیمات خاصی ندارد. فقط کافیست مدل خود را همانطور که آموزش داده شد در نرم افزار رسم کرده و آن را اجرا کنید. در شکل زیر ساده ترین نوع ممکن یک مدل با متغیر میانجی رسم شده است که در آن متغیر توانمند سازی در رابطه میان ارزیابی عملکرد و عملکرد سازمان نقش میانجی را ایفا می کند (در صورت معنادار بودن ضرایب رگرسیونی).

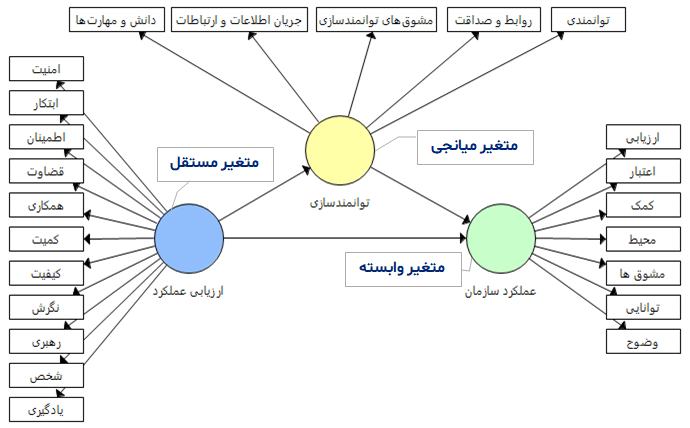
مدل ساده با یک متغیر میانجی

پس از رسم مدل همانطوری که قبل تر آموزش داده شد مدل را از طریق منوی Calculate قسمت بوت استرپینگ اجرا کرده تا پنجره زیر باز شود. پس از تعیین مسیرهای (A) و (B) از طریق آزمون سوبل به بررسی نقش میانجی متغیر توانمندسازی پرداخته می شود. همانطوری که نشان داده شده، با کادر قرمز رنگ ورودی های مورد نیاز برای انجام آزمون سوبل مشخص شده است.

بررسی سوال های شما

سوالم این هست که آیا با PLS میشه مدلی با ۲ متغیر میانجی طراحی کرد و وضعیت میانجی گری ۲ متغیر میانجی رو سنجید ؟ آیا ضرایب در خروجی نرم افزار برای هر متغیر میانجی بصورت مجزا گزارش میشه ؟ برای پاسخ به سوال در شکل زیر مدلی را معرفی می نماییم که در آن دو متغیر میانجی وجود دارد. قصد داریم که تمام حالات ممکن برای نقش میانجی آن ها را بررسی نماییم.

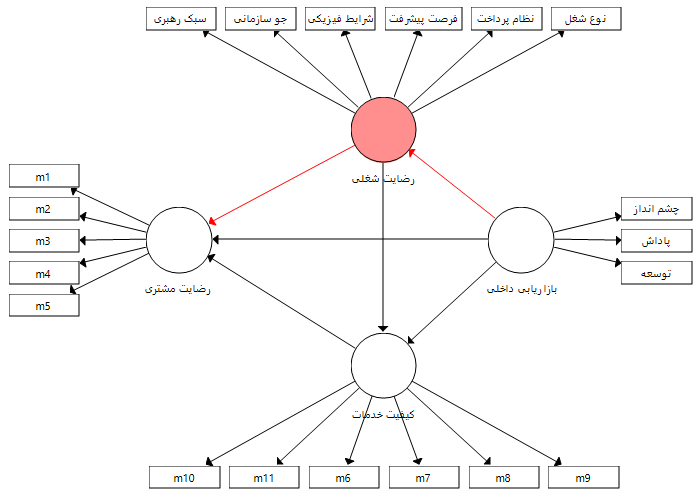
نقش میانجی رضایت شغلی در رابطه میان بازاریابی داخلی و رضایت مشتری

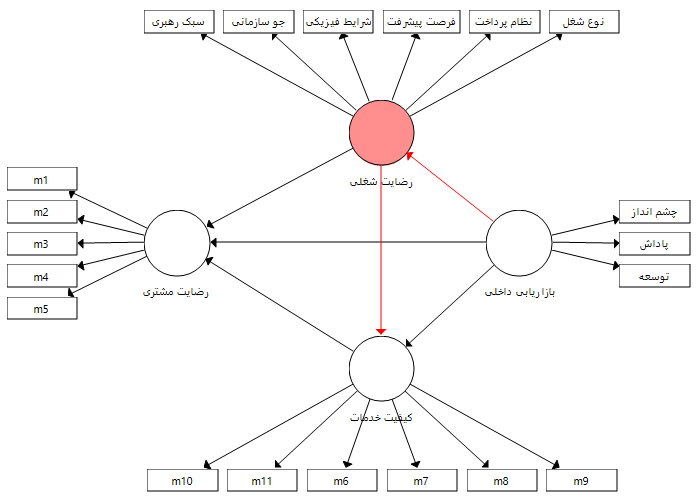
نقش میانجی رضایت شغلی در رابطه میان بازاریابی داخلی و کیفیت خدمات

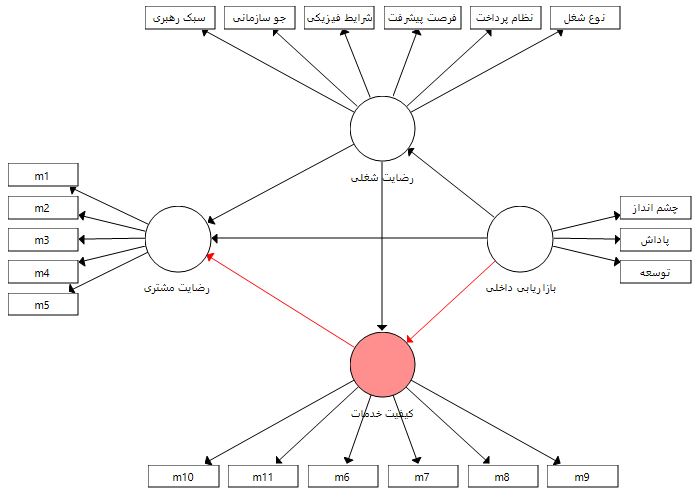
نقش میانجی کیفیت خدمات در رابطه میان بازاریابی داخلی و رضایت مشتری

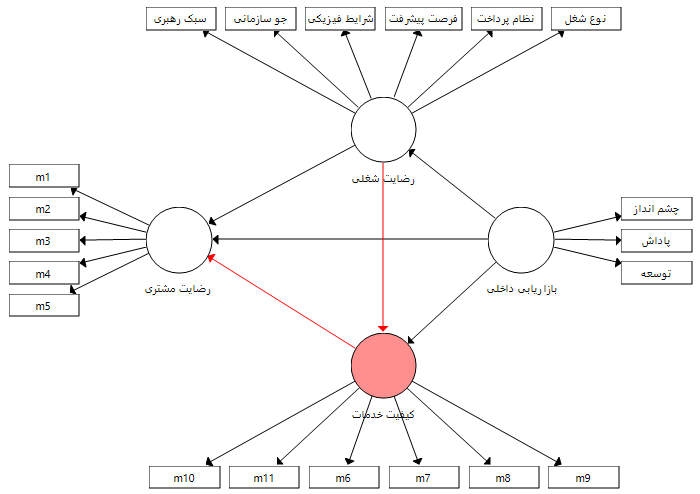
نقش میانجی کیفیت خدمات در رابطه میان رضایت شغلی و رضایت مشتری

بنابراین بر اساس نقش های میانجی متغیرهای کیفیت خدمات و رضایت شغلی می توان چهار فرضیه زیر را مطرح کرد و بر اساس آزمون سوبل هر کدام را جداگانه بر اساس ضرایب و پارامترهای برآورد شده آزمون نمود.

1- بازاریابی داخلی از طریق متغیر میانجی رضایت شغلی بر رضایت مشتری تاثیر دارد.

2- بازاریابی داخلی از طریق متغیر میانجی کیفیت خدمات بر رضایت مشتری تاثیر دارد.

3- بازاریابی داخلی از طریق متغیر میانجی رضایت شغلی بر کیفیت خدمات تاثیر دارد.

4- رضایت شغلی از طریق متغیر میانجی کیفیت خدمات بر رضایت مشتری تاثیر دارد.

نحوه رسم متغیر تعدیلی در نرم افزار SmartPLS

معمولا به این صورت است که برای نشان دادن متغیر تعدیل گر در مدل، از متغیر تعدیل گر فلشی به سمت وسط فلشی که قرار هست آن رابطه را تعدیل کند کشیده می شود. مدل زیر را ملاحظه بفرمایید؛ برای آن که نشان دهیم متغیر تعهد کارکنان زنجیره تامین در رابطه میان رهبری مبادله ای و عملکرد زنجیره تامین و همچنین در رابطه میان رهبری تحول آفرین و عملکرد زنجیره تامین نقش تعدیلی دارد، در مدل مفهومی فلش ها را به صورت زیر رسم می کنیم.

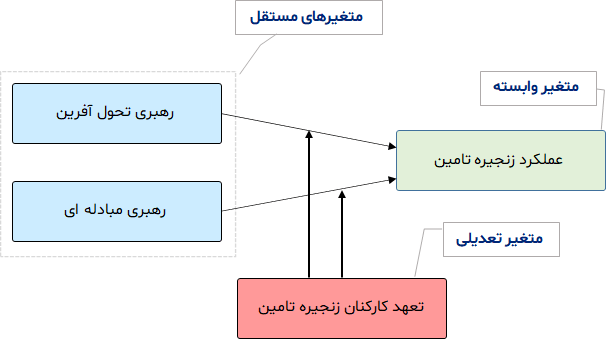
در صورتی که همانطوری که آموزش داده شد در نرم افزار اسمارت PLS برای رسم متغیر تعدیل گر تنظیمات خاصی وجود دارد و شکل ظاهری مدلی که رسم می کنیم با شکل فوق متفاوت خواهد بود. برای رسم مدل دارای متغیر تعدیل گر ابتدا مانند شکل زیر مدل را در نرم افزار رسم می نماییم.

طریقه رسم متغیر تعدیلی در اسمارت پی ال اس

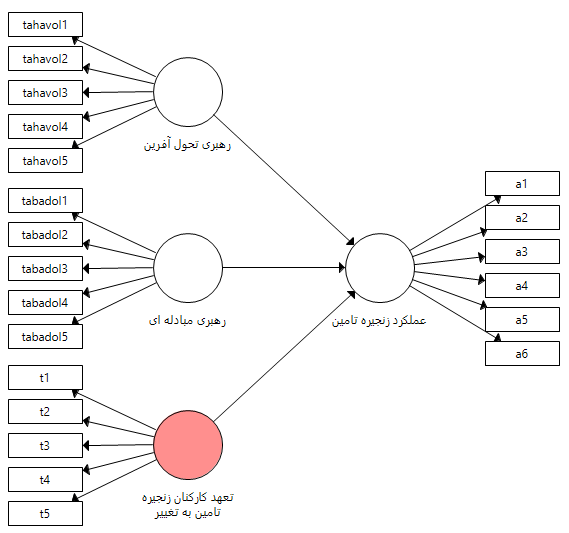
پس از رسم مدل از طریق انتخاب گزینه Moderating effect در کادر بالای نرم افزار و انتخاب متغیر وابسته پنجره زیر باز می شود. در منوی کشویی Moderator Variable متغیر تعهد کارکنان زنجیره تامین را که متغیر تعدیلگر ما هست انتخاب و در منوی کشویی Independent Variable متغیر رهبری تحول آفرین را که یکی از متغیرهای مستقل هست را انتخاب می نماییم. پس از انجام این مراحل بر روی گزینه OK کلیک کرده و مجدد همین کار را برای مستقل دیگر یعنی متغیر رهبری مبادله ای نیز انجام می دهیم.

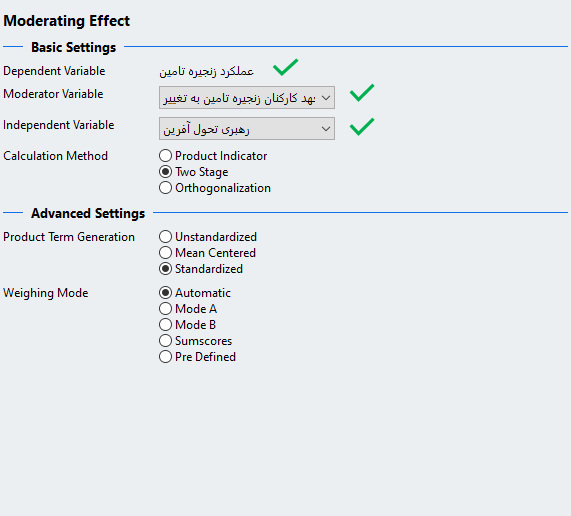
پس از اجرای این تنظیمات بایستی به مدلی مانند شکل زیر دست یابید که در آن از تمامی متغیرها به متغیر وابسته فلش وارد شده است. همانطوری که مشخص است دو متغیر سبز رنگ به مدل اضافه می شود که در واقع ضرب متغیرهای مستقل در متغیر تعدیلی می باشد. شکل زیر نشان دهنده مدل پس از تعریف متغیرهای تعدیلی و تغییر نام آن ها می باشد. در مرحله بعد همانطوری که قبل تر آموزش داده شده مدل اجرا و پارامترها برآورد می شوند.

نمونه مدل دارای متغیر تعدیلی در SmartPLS

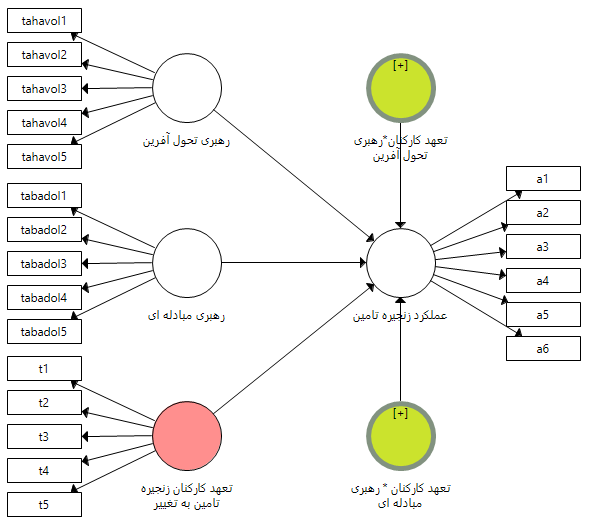
بنابراین بر اساس نقش تعدیلی متغیر تعهد کارکنان عملکرد زنجیره می توان دو فرضیه زیر را مطرح کرد و بر اساس آزمون مدل هر کدام را جداگانه بر اساس ضرایب و پارامترهای برآورد شده آزمون نمود.

1-رهبری تحول آفرین با نقش تعدیلی تعهد کارکنان بر عملکرد زنجیره تامین تاثیر دارد.

2-رهبری مبادله ای با نقش تعدیلی تعهد کارکنان بر عملکرد زنجیره تامین تاثیر دارد.

نحوه رسم مدل تحلیل عاملی مرتبه دوم در SmartPLS

در برخی موارد متغیری در پژوهش داریم که خود از چند زیر مقیاس تشکیل شده است و قصد داریم این متغیر را در نرم افزار رسم کنیم. برای جا افتادن مطلب فرض می کنیم متغیری تحت عنوان مدیریت ریسک داریم که از سه زیر مقیاس امنیت اطلاعات (دارای سه گویه)، تعمیر و نگهداری (دارای سه گویه) و نیروی انسانی (دارای چهار گویه) تشکیل شده است و هدفمان این است که تاثیر متغیر ایمنی آموزش را بر متغیر مدیریت ریسک بررسی کنیم. بنابراین طبق آنچه که آموزش داده شد مدل را به شکل زیر رسم می نماییم.

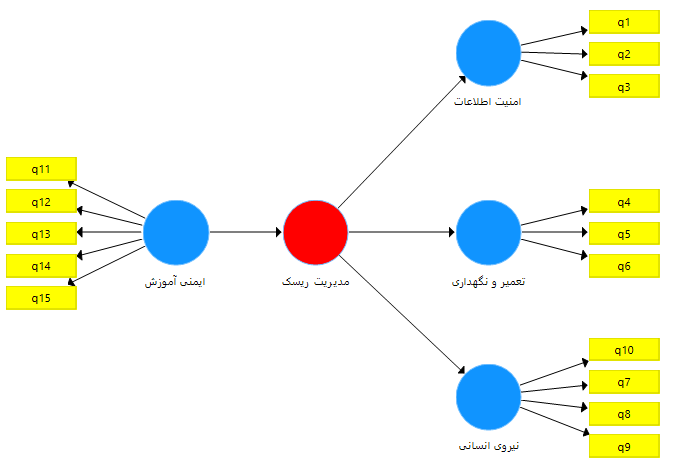
همانطور که ملاحظه می فرمایید متغیر مدیریت ریسک هنوز به رنگ قرمز می باشد و مدل قابل اجرا نیست. برای رفع این مشکل و تعریف متغیر مدیریت ریسک، تمام گویه های مربوطه (گویه های 1 تا 10) را مجددا برای متغیر مدیریت ریسک تعریف می نماییم.

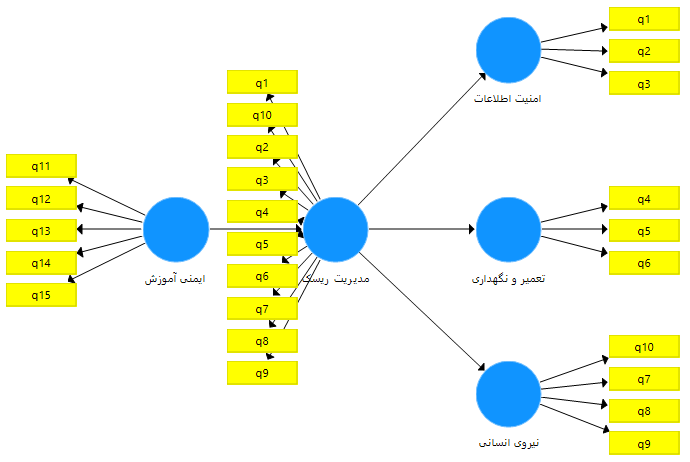
حال بر روی متغیر مدیریت ریسک راست کلیک کرده و گزینه Hide indicators of selected costructs را انتخاب می نماییم. در نهایت مدل به شکل زیر در می آید و قابل اجرا است.

رسم فلش دو طرفه یا کوواریانس (Covariance) در نرم افزار SmartPLS

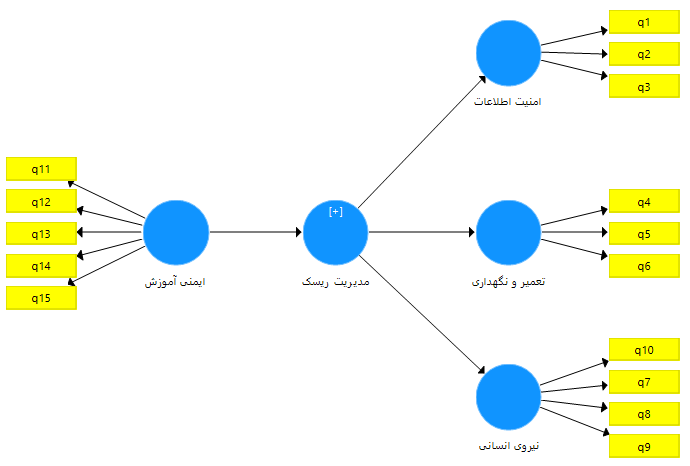
امکان رسم فلش دوطرفه یا فلشی که نشان دهنده ارتباط بین متغیرها می باشد در اسمارت PLS وجود ندارد. در واقع نرم افزار SmartPLS قابلیت اجرای مدل های غیر بازگشتی را ندارد که این یکی از نقاط ضعف این نرم افزار می باشد. در صورتی که این ویژگی در نرم افزارهای کوواریانس محور Amos و Lisrel وجود دارد.

بررسی خطاهای (Error) رایج هنگام کار با نرم افزار SmartPLS

این قسمت به زودی تکمیل خواهد شد.

نحوه مرتب سازی مدل و تغییر فونت با استفاده از ابزارهای SmartPLS

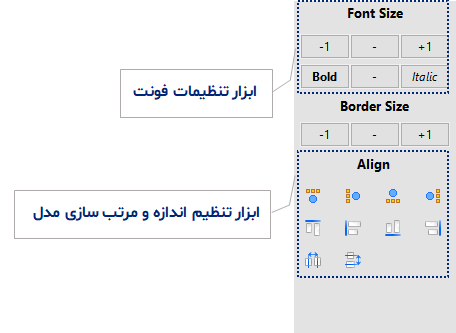
در نرم افزار معادلات ساختاری اسمارت پی ال اس (SmartPLS) ابزارهایی برای مرتب سازی مدل وجود دارد که از این نظر این نرم افزار را نسبت به نرم افزارهای اموس (Amos) و لیزرل (Lisrel) متمایز می نماید. اگر نرم افزار اسمارت PLS نسخه 3 را باز کنید سمت راست پنجره، کادر زیر نمایش داده می شود.

نحوه تغییر رنگ مدل در SmartPLS

همچنین این امکان جالب در نرم افزار SmartPLS وجود دارد که رنگ پیکان ها، متغیرهای پنهان و آشکار و همچنین حاشیه های آن را تغییر داده شده و به رنگ دلخواه درآیند. گوشه بالا سمت راست پنجره اصلی نرم افزار این قابلیت قرار داده شده است :

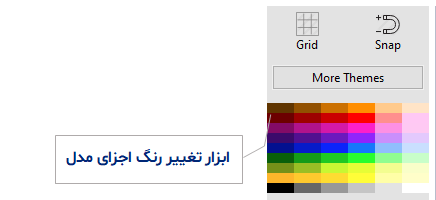
امیدوار هستیم این مطلب برای شما مفید واقع شده باشد، در صورت وجود هرگونه سوال با ما تماس بگیرید.

 

منبع: موسسه آماری کوکرانا- https://cochrana.ir

 

طراحی پرسشنامه آنلاین و رایگان (پرسشنامه الکترونیکی) با سایت پرس لاین www.porsline.ir

معرفی نرم افزار AMOS

IBM® SPSS® Amos یک نرم افزار مدل سازی معادلات ساختاری قدرتمند است که شما را قادر می سازد تا از روش های تحلیلی چند متغیره نظیر رگرسیون، تحلیل عاملی، همبستگی و تحلیل واریانس در تحقیقات و نظریه های خود استفاده کنید. با آموس شما می توانید مدل های نگرشی و رفتاری را ایجاد کنید که رابطه های پیچیده تر را با دقت بیشتری نسبت به تکنیک های آمار چند متغیره با استفاده از رابط کاربری گرافیکی یا محیط برنامه نویسی نشان می دهد.

IBM® SPSS® Amos به شما امکان می دهد تا به راحتی مدل سازی معادلات ساختاری (SEM) را انجام دهید. با استفاده از SEM، شما می توانید به سرعت مدل هایی را برای تست فرضیه ها ایجاد کنید و روابط بین متغیرهای مشاهده شده و پنهان را تأیید کنید.

مدل سازی معادلات ساختاری (SEM) می تواند تحقیقات شما را به سطح بعدی برساند.

وقتی تحقیق میکنید، احتمالا از تجزیه و تحلیل عوامل و رگرسیون استفاده میکنید. مدل سازی معادلات ساختاری (گاهی اوقات به نام تجزیه و تحلیل مسیر هم شناخته می شود) می تواند به شما در درک بهتر مدل های علی کمک کند و اثرات متقابل و مسیرهای بین متغیرها را کشف کند. SEM به شما اجازه می دهد تا دقیق تر آزمون کنید که آیا اطلاعات شما از فرضیه شما پشتیبانی می کند یا خیر.

IBM SPSS Amos یک ابزار مدل سازی کامل است که برای اهداف مختلف مورد استفاده قرار میگیرد. از جمله:

روانشناسی: مدل هایی را برای درک اینکه چگونه درمان های دارویی، بالینی و هنر بر خلق و خوی تاثیر می گذارد، بسازید
تحقیقات پزشکی و بهداشتی: تأیید کنید که کدام یک از سه متغیر  اعتماد به نفس، صرفه جویی یا تحقیق، بهترین پیش بینی کننده حمایت پزشک برای تجویز داروهای عمومی است
علوم اجتماعی: بررسی وضعیت وضعیت اجتماعی، عضویت سازمانی و سایر عوامل تعیین کننده در تفاوت در رفتار رای گیری و مشارکت سیاسی
تحقیقات آموزشی: ارزیابی نتایج برنامه آموزشی جهت تعیین تأثیر بر اثربخشی کلاس درس
تحقیق بازار: مدل چگونگی رفتار مشتری بر فروش محصول جدید و یا تحلیل رضایت مشتری و وفاداری برند
تحقیقات سازمانی: بررسی اینکه چگونه مسائل مربوط به کار بر رضایت شغلی تاثیر می گذارد
برنامه ریزی کسب و کار: ایجاد مدل های اقتصاد سنجی و مالی و تجزیه و تحلیل عوامل موثر در دستیابی به شغل در محل کار
ارزیابی برنامه: ارزیابی نتایج برنامه یا مدل رفتاری با استفاده از SEM برای جایگزینی رگرسیون گام به گام سنتی

محاسبه حجم نمونه آماری با استفاده از فرمول کوکران

فرمول کوکران یکی از مؤلفه های مهم در روش شناسی، جامعـه و نمونـه آمـاری اسـت.

اگـر بـه دلیـل محدودیت زمان، بودجه و نیروی انسانی، امکان بررسی کل اعضای جامعه آمـاری فـراهم نباشـد باید از نمونه گیری و در غیر این صورت از سرشماری استفاده کرد.

به طور طبیعی نتایج سرشماری در مقایسه با نمونه گیری بسیار دقیق تر است؛ چرا که خطای نمونـه گیـری وجـود نـدارد. در روش سرشماری، از شاخص های آمار توصیفی و ساده ای مانند میانگین یا واریانس استفاده می شود، امـا در روش نمونه گیری، از روش های آمار استنباطی و آزمون های آماری استفاده می شـود. بـه دلیـل پیچیدگی و جذابیت ظاهری روش های استنباطی، گرایش دانشجویان و اسـاتید بـه آن بیشـتر از آمار توصیفی است؛ به گونه ای که حتی در حالت سرشماری هم از روش هـای اسـتنباطی اسـتفاده شده است. در موارد متعدد مشاهده می شود که محقق قادر به سرشماری است، اما به دلیل ایجـاد توجیهی به منظور استفاده از آزمونهای آماری، اقدام به نمونه گیری می کند.

در نمونه گیری محقق با دو سؤال اساسی روبه روست: چند واحد نمونه گیری انتخاب شوند؟ چگونه واحدهای نمونه گیری از بین جامعه آماری انتخاب شوند؟ در پاسخ به سؤال اول بایـد حجـم نمونـه مشـخص شـود. در تعیین حجم نمونه دو رویکرد عمده وجود دارد.
رویکرد فرمولی: در این حالت از فرمولهای مختلف ارائه شده ویلیام کـوکران در سـال ۱۹۷۷ استفاده می شود.  که در سایت زیر با محاسبه آنلاین حجم نمونه با فرمول کوکران می توان از سایت زیر استفاده نمود:

http://tahlileamari.ir

رویکرد جدولی: در این رویکرد جدول تعیین حجم نمونه کرجسی و مورگان (۱۹۷۰) اسـتفاده می شود.

تحلیل عاملی تاییدی مرتبه دوم با LISREL

تحلیل عاملی تاییدی مرتبه دوم با نرم افزار AMOS

نرم افزار SPSS چیست؟

نرم افزار SPSS یک نرم افزار بسیار قدرتمند در زمینه  آمار می باشد. شما به راحتی می توانید انواع آمار توصیفی و استنباطی را به وسیله این نرم افزار به انجام برسانید. این نرم افزار برای افرادی که در حال انجام پایان نامه کارشناسی ارشد و دکترا هستند علی الخصوص در رشته های علوم انسانی، مدیریت دولتی، مدیریت آموزشی، مدیریت فرهنگی، برنامه ریزی درسی، علوم تربیتی، روان شناسی و پزشکی بسیار مفید و حتی ضروری است.

قابلیت‌های نرم افزار SPSS  به ‌شرح زیر است:

• تهیه خلاصه‌های آماری مانند گراف‌ها، جداول‌، آماره‌ها و …

• انواع توابع ریاضی مانند قدر مطلق، تابع علامت، لگاریتم، توابع مثلثاتی و …

• تهیه انواع جداول سفارشی مانند جداول فراوانی، فراوانی تجمعی، درصد فراوانی و …

• انواع توزیع‌های آماری شامل توزیع‌های گسسته و پیوسته

• تهیه انواع طرح‌های آماری

• انجام آنالیز واریانس یکطرفه، دوطرفه، چندطرفه و آنالیز کوواریانس

• تکنیک‌های تجزیه و تحلیل سری‌های زمانی

• ایجاد داده‌های تصادفی و پیوسته

• محاسبه انواع آماره‌های توصیفی

• انواع آزمون‌های مرتبط با مقایسه میانگین بین دو یا چند جامعه مستقل و وابسته

• قابلیت مبادله اطلاعات با نرم‌افزارهای دیگر

• برازش انواع مختلف رگرسیون

• و ……

تفاوت های مهم میان پژوهش کیفی و پژوهش کمی

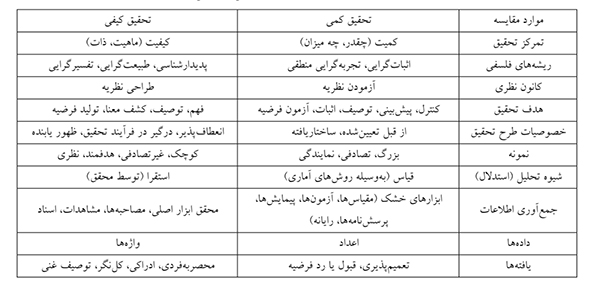
جدول زیر تعدادی از تفاوت های عمده میان پژوهش های کیفی و کمی را نشان می دهد:

                                           

 

اهمیت انتخاب صحیح روش های آماری در پروپوزال نویسی روانشناسی

 

اولا، انتخاب روش آماری برای هر فرضیه مطرح شده باید بصورت منطقی صورت گیرد، در غیر این صورت تفسیر معناداری نمی تواند از نتایج به دست آمده صورت گیرد.

مثلا، اگر پژوهشگری قصد بررسی تفاوت میانگین های نمرات دو گروه را داشته باشد و روش آماری همبستگی میان متغیرها را برگزیند، تفسیر او از نتایج اساساً بی معنا خواهد بود.

بطور عمده بر اساسی دو اصل کلی انتخاب می شود:

مقیاس اندازه گیری به کاربرده شده در سنجش متغیرها. در نتیجه، پژوهنده پیش از آن که تصمیم بگیرد داده های خود را تحلیل کند باید بتواند معین کند که فرضیه یا فرضیه های مورد نظر، هریک چه ماهیتی دارد؟

این داده ها از چه نوع است؟

وی باید آگاه باشد که سازمان دادن، خلاصه کردن و نمایش داده ها، بستگی به سطح و مقیاس اندازه گیری متغیر (اسمی، رتبه ای، فاصلهای و نسبی) دارد.

هدف از انجام تحقیق های کیفی

هدف پژوهش های کیفی درک پدیده ها در بستر نهادی و اجتماعی خاص آنها است.

هدفی که با رویکردهای کمی چندان قابل وصول نیست.

به اعتقاد پژوهشگران کیفی، واژه «آزمودنیها» باید به «مشارکت کنندگان» تبدیل شوند و افراد نه برای تأیید دانش قیاسی خود بلکه برای مطالعه و فهم نقش آنها در بستر خاص خود فهم کرد .

در پژوهش های از نوع کیفی، در صورت استفاده از روش مصاحبه، تعیین نوع سؤال های مصاحبه با توجه به متغیرهای پژوهش، آن هم قبل از انجام مصاحبه و توجه به شیوه های کدگذاری (اعم از کد گذاری از نوع باز یا واقعی، کدگذاری محوری، نظری و کد گذاری انتخابی) بنا به اقتضاء، ضرورت دارد.

در صورت امکان ضبط مصاحبه ها میتواند در فرصت مناسب امکان تحلیل آن را برای پژوهشگر فراهم نماید .

تنظیم و تحلیل داده های کیفی مستلزم سه فعالیت است:

الف) تلخیص داده ها

ب) عرضه داده ها

ج) نتیجه گیری و تأیید

طی دهه های اخیر توجه به رویکردهای مختلف از جمله پژوهش کیفی به طور فزاینده ای مورد استفاده قرار می گیرد.

اصولأ، لزوم توجه به این گونه تحقیقات را که مطالعه انسانی در متن جامعه و نگاه همزمان به انسان، محیط و همه متغیرهای تأثیرگذار ہر آن را مورد تأکید قرار می دهد، خاطر نشان ساخته است.

پژوهش کیفی در جست و جوی پدیده ها یا حوزه های پیچیده است که رویکرد مطالعه به شیوه کمی چندان مؤثر نیست.

چه زمانی از انواع آزمون تی t استفاده می کنیم؟

آزمون تی ، یک آزمون استنباطی برای تحلیل داده های پارامتری است. هدف از آزمون تی t برای بررسی تفاوت بین میانگین های دو گروه مستقل است که پژوهشگر را در زمینه تصمیم گیری یاری کند.

پژوهشگر باید تصمیم بگیرد که تفاوت مشاهده شده بین دو میانگین نمونه (به عنوان مثال گروه های آزمایش و گواه) در اثر عوامل شانس به وجود آمده یا تفاوت مشاهده شده بیانگر تفاوت واقعی بین دو جامعه است.

به بیانی، این آزمون برای ارزیابی یکسان بودن و نبودن میانگین نمونه ای با میانگین جامعه در حالتی به کار مرود که انحراف معیار جامعه مجهول باشد، چون توزیع t در مورد نمونه های کوچک با استفاده از درجات آزادی تعدیل می شود، می توان از این آزمون برای نمونه های بسیار کوچک استفاده نمود.

هم چنین این آزمون مواقعی که خطای استاندارد جامعه نامعلوم و خطای استاندارد نمونه معلوم باشد، کاربرد دارد برای به کاربردن این آزمون، متغیر مورد مطالعه باید در مقیاس فاصله ای باشد، شکل توزیع آن نرمال باشد.

به عنوان مثال، پژوهشگری نمونه های مورد نیاز را به طور تصادفی از بین دانش آموزان همتا انتخاب کرده است و درصدد است تأثیر یک روش خاص تدریس را بر پیشرفت یا عملکرد تحصیلی آن ها، ارزیابی کند.

روش تدریس مورد نظر در چندین جلسه در باره گروه آزمایش اجرا می شود، در حالی که گروه گواه بر کنار از این تأثیر می باشد.

در این شرایط، معنادار بودن تفاوت بین دو میانگین از نظر پیشرفت تحصیلی را می توان به وسیله آزمون تی t برای میانگین های مستقل تعیین کرد.

به کارگیری آزمون تی t در پژوهش های علی - مقایسه ای وابسته به سه پیش فرض می باشد:

۱. نمره ها براساس مقیاس فاصله ای یا نسبی باشد؛

۲. توزیع نمره ها در جامعه پژوهش دارای توزیع نرمال باشد (توزیع طبیعی باشد):

۳. واریانس نمره ها در دو جامعه پژوهش برابر باشد (میانگین توزیع برابر صفر است).

روش های آزمون تی t مختلف است که شامل تی با یک مقدار معین (تی صفر)، تی مستقل و تی وابسته می شود.

 

الف) تی با مقدار معین

این آزمون بررسی میکند که آیا میانگین مشاهده شده در مقایسه با یک مقدار معین (معمولاً حد متوسط که توسط پژوهشگر قابل تعیین و تغییر است) متفاوت است یا خیر؟

در این آزمون مقایسه یک عدد فرضی (میانگین نظری) با میانگین جامعه نمونه مورد نظر است.

به عبارتی، زمانی که پژوهشگر علاقه مند است که ببیند آیا میانگین یک نمونه با میانگین یک جامعه مشخص شده تفاوت معنادار دارد یا خیر از آزمون تی t برای با مقدار معین استفاده می کند و هم چنین زمانی که مقدار خطای معیار میانگین نامعلوم است و مقدار آن از طریق داده های به دست آمده گروه نمونه برآورد می شود، می توان از این آزمون استفاده کرد.

آزمون تی t، وسیله ای است برای اندازه گیری تفاوت بین میانگین نمونه و میانگین جامعه برحسب واحد خطای معیار که این واحد از طریق داده های به دست آمده از گروه نمونه برآورد می شود.

شرط استفاده از توزیع نمونه گیری با جهت آزمون فرضیه ها چند شرط دارد:

۱. نمره ها به صورت نمونه گیری تصادفی از جامعه مورد نظر انتخاب شده باشد:

۲. شکل توزیع پراکندگی نمره ها در جامعه نرمالی باشد (از نظر شکلی متقارن باشند). فرض کنید که پژوهشگری یک نمونه از دانش آموزان کلاسی را که داری ویژگیهای مشترکی هستند مطالعه می کند.

این تحقیق، یک آزمون هوشی (مانند آزمون وکسلر) را برای آنها اجرا کند و میانگین بهره هوشی کلاس برابر ۱۰۹ به دست می آید.

این پژوهشگر به عنوان بخشی از تحلیل یافته ها علاقه مند است بداند که آیا بین این میانگین (۱۰۹) و میانگین جامعه تفاوت معناداری وجود دارد یا خیر.

اگر فرض شود که میانگین جامعه برابر ۱۰۰ است، می توان از آزمون تی t برای یک میانگین استفاده نمود و تفاوت بین ۱۰۰ (میانگین جامعه) و ۱۰۹ (میانگین نمونه) را از نظر معنادار بودن آماری مشخص نمود.

 

ب) تی با نمونه مستقل

ان دسته از طرح هایی که در ان دو متغیر و یا نمونه مستقل در دو موقعیت مورد ازمون ومقایسه قرار می گیرد.

مانند بررسی تاثیر دو روش تدریس (فعال و غیر فعال) در پیشرفت تحصیلی دانش آموزان، در این مثال میانگین ها و نمونه ها مستقل از هم فرض می شود.

 

ج) تی زوجی یا وابسته

آن دسته از طرح هایی که در آن یک متغیر مستقل در دو موقعیت مورد آزمون قرار گیرد و در این دو موقعیت، آزمودنیهای یکسان یا همتا شرکت داشته باشند، از از مونتی زوجی یا وابسته استفاده میشود.

این ازمون «مقایسه زوج ها» هم نامیده می شود.

برای مثال، جهت بررسی تاثیر روش تدریس بر یادگیری ازمودنیها و برای تعیین معنادار بودن تفاوت بین نمره ها در قبل و بعد اجرای روش تدریس، از از مونتی برای مقایسه دو میانگین همبسته (زوج ) استفاده می شود و طرحی که برای ارزشیابی استفاده می شود پیش ازمون و پس ازمون است.

یا اینکه پژوهشگری قصد دارد وضعیت موجود و مطلوب جو یک سازمان را مورد بررسی قرار دهد و دریابد که ایا بین این دو وضعیت با توجه به نظر و ارزش گذاری مدیران، تفاوت وجود دارد یا نه؟

به این منظور، وی تعدادی از مدیران را به طور تصادفی انتخاب و نظر آنان را درباره ارزش گذاری وضعیت جو سازمان، جویا می شود.

یعنی هر مدیر، هم زمان درباره جو موجود و نیز مطلوب سازمان اظهار نظر می کند.

سپس این تفاوت تحلیل آماری می شود. مزیت این آزمون در آن است که در مقایسه با آزمون تی t برای میانگین های مستقل، در این آزمون خطای معیار کمتری وجود دارد.

در نتیجه احتمال بیشتری وجود دارد که پژوهشگر بتواند تفاوت معناداری را بین میانگین ها به دست آورد.

توزیع تی چیست؟

توزیع t نیز مانند توزیع نرمال قرینه است ولی دارای پراکندگی بیشتری نسبت به توزیع نرمال است. و برای مقادیر مختلف حجم نمونه (n) میزان پراکندگی توزیع t تغیر می کند و با افزایش حجم نمونه این پراکندگی کمتر شده و برای  توزیع t با توزیع Z برابر می شود.
بنابراین شکل این توزیع به حجم نمونه بستگی دارد که انرا با r نشان داده و درجه آزادی می نامیم.

در شکل زیر سطح زیر منحنی در دنباله راست توزیع t، با توجه به پارامتر درجه آزادی ثبت شده است.

برای استفاده از جدول t فوق احتیاج به دو عدد

• سطح منحنی در دنباله سمت راست توزیع
• درجه آزادی توزیع t داریم

ما حرف t_a,r را به مفهوم مقدار t با سطح زیر منحنی a و درجه آزادی r به کار می بریم.
مثال: اگر a=0.025 و r=15 باشد مقدار t را به دست آورید.

t_0.025,15=2.131

برای پیدا کردن عدد 2.131 در جدول t کافی است که از سطر اول جدول، عدد 0.025 و از ستون اول جدول درجه آزادی 15 را پیدا کنیم محل برخورد سطر و ستون عدد 2.131 را ارائه می کند.

نکته:
اگر جامعه مورد بررسی نرمال و انحراف معیار جامعه معلوم نباشد و نمونه تصادفی به حجم n از جامعه اختیار کنیم ان گاه آماره

که در آن  و  است دارای توزیع t با n-1 درجه آزادی است.
سوال: چرا درجه آزادی برابر n-1 است؟
در توجیه درجه آزادی به مثال زیر توجه کنید اگر n=5 و = 8 باشد بنابراین جمع این 5 مشاهده باید برابر 40 باشد. فرض کنید بخواهیم این مجموعه اعداد را مشخص کنیم. برای این کار می توانیم هر چهار عددی که دوست داریم به صورت آزادانه انتخاب کنیم ولی هیچگونه آزادی در انتخاب عدد پنجم نداریم زیرا عدد پنجم را باید بگونه ای انتخاب کرد که جمع 5 عدد برابر 40 شود. بنابراین درجه آزادی ما برابر 4 است.

سرفصل های آمار استنباطی

روش های نمونه گیری:

نمونه گیری تصادفی ساده

نمونه گیری منظم یا سیستماتیک

نمونه گیری طبقه ای

نمونه گیری خوشه ای

خطای نمونه گیری

خطای استاندارد میانگین

خطای استاندارد میانه

خطای استاندارد نسبت

خطای استاندارد انحراف استاندارد

خطای استاندارد فراوانی

 

آزمون فرضیه:

فرض صفر

فرض خلاف

خطای نوع اول

خطای نوع دوم

توان آزمون

سطح اطمینان

آزمون های یک دامنه و دو دامنه

تفسیر تایید یا ردفرض صفر

 

آزمون های t:

توزیع t استودنت

درجات آزادی

ویژگی های توزیع t استودنت

استفاده از توزیع t در آزمون فرضیه

آزمون فرضیه درباره میانگین جامعه (آزمون یک گروهی)

توزیع t برای معنادار بودن اختلاف بین میانگین ها

توزیع تفاوت بین دو میانگین

خطای استاندارد تفاوت بین دو میانگین

توزیع t برای تفاوت بین میانگین های دو نمونه

توزیع t برای گروه های همبسته

مقایسه توان آزمون ها

 

آزمون های معنادار بودن: نسبت، واریانس و همبستگی:

آزمون نسبت

آزمون معنادار بودن مقایسه یک نسبت با یک نسبت ثابت

آزمون معنادار بودن تفاوت بین دو نسبت مستقل

آزمون معنادار بودن تفاوت بین دو نسبت همبسته

آزمون واریانس

مقایسه واریانس های مستقل

آزمون معنادار بودن همبستگی

آزمون معنادار بودن ضریب همبستگی

آزمون معنادار بودن تفاوت دو ضریب همبستگی در نمونه های مستقل

آزمون معنادار بودن تفاوت بین دو ضریب

همبستگی در نمونه های همبسته

 

تجزیه و تحلیل واریانس یک طرفه:

برآورد واریانس جامعه

نسبت F

مقایسه میانگین ها پس از آزمون F

مفروضه های تجزیه و تحلیل واریانس

 

طرح های بلوکی تصادفی:

آزمون معنادار بودن در طرح بلوکی تصادفی شده

دسته بندی کردن آزمودنی ها در بلوک ها

 

تحلیل واریانس اندازه گیری مکرر:

مجموع مجذورات و درجات ازادی

 

آزمون های تعقیبی:

دامنه استودنت شده

آزمون چنددامنه ای دانکن

آزمون نیومن کلز

آزمون توکی

آزمون شفه

 

طرح عاملی:

طرح عاملی واکنش متقابل

اثرات اصلی و کنش متقابل

درجات ازادی، میانگین مجذورات و آزمون F

 

آزمون خی دو:

نیکویی برازش خی دو

درجات ازادی

تصحیح خی دو

درجات ازادی برای جداول توافقی

ضریب فی

ضریب توافقی

واریانس و انحراف معیار به زبان ساده

ابتدا و پیش از هر چیزی اجازه دهید به این پرسش پاسخ دهیم که انحراف معیار چیست؟ انحراف معیار (Standard deviation) از دو واژه تشکیل یافته است. جزء اول یعنی انحراف به میزان دوری هر عضو یک مجموعه داده از مقدار میانگین گفته می‌شود. واژه معیار نیز به معنی استاندارد بودن این مقدار است. هر چه انحراف معیار مجموعه‌ای از داده‌ها عدد پایین‌تری باشد، نشانه آن است که داده‌ها به میانگین نزدیک هستند و پراکندگی اندکی دارند. در صورتی که انحراف معیار عدد بزرگی باشد، نشان می‌دهد که پراکندگی داده‌ها زیاد است. پس انحراف معیار، عددی برای نشان دادن میزان پراکندگی اعضای یک مجموعه از داده‌ها است.

انحراف معیار به چه دردی می‌خورد؟

انحراف معیار مفهومی است که میزان پراکندگی داده‌های یک مجموعه را مشخص می‌کند و بدین جهت یکی از مهم‌ترین مقیاس‌های آماری در زمینه آمار توصیفی به حساب می‌آید. اگر میانگین برآوردی از نقطه ثقل توزیع داده‌های یک مجموعه به دست می‌دهد، و از این رو مقیاسی تک‌بعدی برای برآورد یک مجموعه داده‌ها فراهم می‌سازد، می‌توان گفت که انحراف معیار نیز میزان پراکندگی داده‌ها از نقطه میانگین را نشان می‌دهد و از این رو مقیاسی دوبعدی برای برآورد توزیع داده‌ها در اختیار ما قرار می‌دهد.

مثال

برای مثال اگر یک معلم هستید، احتمالاً برایتان مهم است که بدانید دانش‌آموزان شما در امتحانی که اخیراً گرفته‌اید چه عملکردی داشته‌اند. اگر ۲۰ یا ۳۰ دانش‌آموز داشته باشید با نگاه کردن به تک‌تک نمرات شاید نتوانید برآورد صحیحی از عملکرد کل کلاس به دست آورید، ولی مسلماً در صورتی که میانگین نمره‌های همه دانش‌آموزان را محاسبه کنید، می‌توانید بدانید که وضعیت کل کلاس چگونه بوده است. برای مثال اگر میانگین نمره‌های کلاس برابر با ۱۲٫۵ باشد و میانگین محاسبه شده برای امتحان قبلی ۱۴ بوده باشد، نشان دهنده افت نمرات است و نیاز به چاره‌جویی وجود دارد.

شما به عنوان یک معلم باید با کدام دانش‌آموزان بیشتر کار کنید؟ مسلماً برای دانش‌آموزانی که عملکرد بهتری دارند نیاز چندانی به تلاش بیشتر وجود ندارد، اما به دانش‌آموزانی که عملکرد ضعیف‌تری دارند می‌بایست توجه ویژه‌ای صورت بگیرد. اما چگونه می‌توان فهمید که کدام دانش‌آموزان عملکرد بالاتر دارند، متوسط هستند یا عملکرد ضعیف‌تری دارند؟ پاسخ به این سؤال از طریق محاسبه انحراف معیار است. انحراف معیار مقیاسی به دست می‌دهد که با استفاده از آن می‌توانیم بدانیم میانگین اختلاف عملکرد دانش‌آموزان از نقطه میانگین کلاسی چقدر است.

برای مثال فرض کنید در کلاس شما انحراف معیار برابر با ۲٫۵ باشد. اگر توزیع نمرات دانش‌آموزان به صورت یک توزیع نرمال باشد (که در اغلب موارد در مورد چنین اندازه‌گیری‌هایی از توزیع نرمال پیروی می‌کند)، این عدد نشان می‌دهد که نمرات بیش از دو سوم یا ۶۸٫۲% از دانش‌آموزان شما در محدوده ۲٫۵ + ۱۲٫۵ قرار دارد. این عدد طبق تعریف انحراف معیار به دست می‌آید. یک سوم دیگر از دانش‌آموزان یا نمراتی بالاتر از ۱۵ کسب کرده‌اند که طبعاً نیاز چندانی به تلاش بیشتر شما ندارند و یا نمراتی زیر ۱۰ کسب کرده‌اند که مسلماً نیازمند توجه ویژه هستند. بدین ترتیب با محاسبه انحراف معیار نمره‌های کلاسی می‌توانید دانش‌آموزان را به سه دسته ضعیف (کمتر از ۱۰)، متوسط (۱۰ تا ۱۵) و قوی (بالاتر از ۱۵) تقسیم‌بندی کنید.

فرض کنید در مثال فوق تعداد دانش‌آموزانی که نمرات زیر ۱۰ کسب کرده بودند یعنی مردود بودند برابر با ۵ بوده است. همچنین فرض می‌کنیم معلم با این دسته از دانش‌آموزان تمرین می‌کند ولی در امتحان بعدی میانگین نمرات کلاس هنوز همان ۱۲٫۵ است. شاید در نگاه اول به نظر برسد، تلاش‌های وی بی‌نتیجه بوده است؛ اما با محاسبه انحراف معیار می‌بینیم که این عدد به ۱ کاهش یافته است، یعنی نمرات بیش از دوسوم کلاس در محدوده ۱ + ۱۲٫۵ قرار دارد. این به آن معنی است که به احتمال بسیار زیاد تعداد دانش‌آموزانی که نمره زیر ۱۰ کسب کرده‌اند، کاهش یافته است.

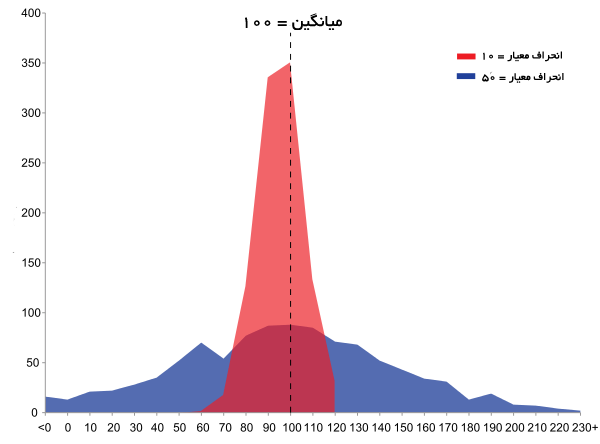
در تصویر فوق به خوبی اهمیت مفهوم انحراف معیار در برآورد توزیع داده‌ها را می‌بینید. هر دو مجموعه داده‌های آبی و قرمز رنگ میانگینی برابر با ۱۰۰ دارند ولی انحراف معیار مجموعه داده‌های آبی ۵ برابر داده‌های قرمز است. علامتی که برای نشان دادن انحراف معیار استفاده می‌شود، حرف یونانی سیگما ” σ ” است. روشی که عموماً برای محاسبه انحراف معیار استفاده می‌شود از طریق جذر گرفتن از واریانس است. خب اکنون شاید بپرسید واریانس چیست؟

واریانس چیست؟

واریانس به صورت «مقدار متوسط مربع اختلاف مقادیر از میانگین» تعریف شده است. شاید در نگاه نخست تعریف دشواری به نظر برسد! اما هیچ جای نگرانی نیست چون در عمل خواهید دید که مفهوم بسیار ساده‌ای است.

برای محاسبه واریانس، باید گام‌های زیر را دنبال کنید:

• ابتدا میانگین را پیدا کنید (میانگین ساده اعداد).
  سپس برای هر عدد، مقدار میانگین را از آن تفریق کرده و سپس نتیجه را به توان دو برسانید (مربع اختلاف).
  و در نهایت میانگین مربع اختلافات به دست آمده را محاسبه کنید.

واریانس داده‌ها آماده است. به همین سادگی!

مثال

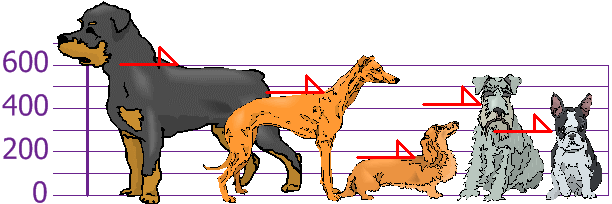
فرض کنید متصدی یک محل نگهداری از سگ‌ها می‌خواهد قد سگ‌های موجود را به منظور خاصی اندازه‌گیری کند. نتایج این اندازه‌گیری قد (از شانه) به شرح زیر است:

۳۰۰، ۴۳۰، ۱۷۰، ۴۷۰ و ۶۰۰ میلی‌متر

اینک می‌خواهیم میانگین، واریانس و انحراف معیار این داده‌ها را پیدا کنیم. گام اول یافتن میانگین است:

پس میانگین قد همه سگ‌ها برابر با ۳۹۴ میلی‌متر است. اکنون خط میانگین را روی شکل رسم می‌کنیم:

اکنون اختلاف قد هر کدام از سگ‌ها را از مقدار میانگین حساب می‌کنیم:

برای محاسبه واریانس، اختلاف تک‌تک داده‌ها را به توان دو رسانده و سپس میانگین می‌گیریم:

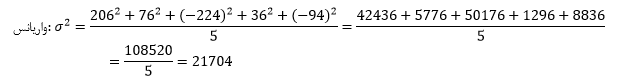
پس، واریانس برابر است با: ۲۱۷۰۴

و انحراف معیار همان جذر واریانس است، پس:

و اما نکته خوب در مورد انحراف معیار، سودمند بودن آن است. اکنون می‌توانیم بفهمیم قد کدام سگ‌ها در محدوده یک انحراف معیار میانگین (۱۴۷ میلی‌متر) قرار دارد.

پس با استفاده از انحراف معیار، ما یک راه “استاندارد” برای یافتن محدوده مقادیر نرمال، مقادیر بیش از نرمال و مقادیر کمتر از نرمال در دست داریم.

اما زمانی که به همه اعضای یک مجموعه دسترسی نداشته باشیم از نمونه‌گیری استفاده می‌کنیم. نمونه‌گیری به معنی انتخاب تصادفی برخی از اعضای یک مجموعه بزرگ (جامعه آماری نامیده می‌شود) است که در محاسبه‌های آماری به عنوان مثالی گویا از کل نمونه در نظر گرفته می‌شود و در این حالت برای محاسبه انحراف معیار و واریانس تفاوتی اندک وجود دارد. برای نمونه در مثال سگ‌ها مجموعه داده‌های ما مربوط به یک جمعیت بود (۵ سگ تنها سگ‌های مورد بررسی بودند). اما اگر داده‌های ما یک نمونه یعنی یک جمعیت کوچک در نظر گرفته شده از یک جمعیت بزرگ‌تر، برای مثال ۵ سگ که از میان ۵۰ سگ به صورت تصادفی انتخاب شده‌اند باشد، در این صورت محاسبات تغییر می‌یابند.

وقتی N داده وجود داشته باشند، هنگام محاسبه واریانس مجموع مربعات اختلاف از میانگین‌ها بر N تقسیم می‌شوند. اما هنگامی که قرار باشد این محاسبات بر روی نمونه‌ای از یک جامعه آماری انجام یابد مجموع مربعات اختلاف از میانگین‌ها بر N-1 تقسیم می‌شود. در این حالت باقی محاسبات از جمله روش محاسبه میانگین به همان شکل می‌ماند.

مثال: اگر ۵ سگ موجود فقط نمونه‌ای از جمعیت بزرگ‌تر سگ‌ها باشد، مقدار را به جای ۵، باید بر ۴ تقسیم کنیم:

واریانس نمونه: ۱۰۸۵۲۰/۴ = ۲۷۱۳۰

انحراف معیار نمونه = ۲۷۱۳۰√ = ۱۶۴ (نزدیک‌ترین داده)

دلیل این منهای یک کردن، خارج از حوصله این نوشته است و برای اطلاعات بیشتر می‌توانید به لینک‌های انتهای نوشته مراجعه کنید.

فرمول‌ها:

در ادامه فرمول‌های ریاضی حالت کلی محاسبه انحراف معیار برای هر دو حالت جمعیت و نمونه آماری ارائه شده است:

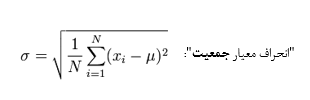
گرچه پیچیده به نظر می‌آید، اما ما قبلاً آن را به طرز بسیار ساده‌ای محاسبه کرده‌ایم. تنها تفاوت مهم، تقسیم‌بر N-1 (بجای N) هنگام محاسبه واریانس نمونه است.

چرا اختلاف از میانگین‌ها را به توان دو می‌رسانیم؟

اگر ما تنها اختلاف‌ها را میانگین‌گیری می‌کردیم… اعداد منفی، اعداد مثبت را خنثی می‌کردند:

پس این راه‌حل درست نیست. اما آیا از قدر مطلق مقادیر می‌توانیم استفاده کنیم؟

همان‌طور که می‌بینید به نظر می‌رسد انحراف میانگین به طور صحیحی محاسبه شده است؛ اما در مورد حالت زیر چه می‌توان گفت؟

می‌بینید که مقدار انحراف معیار همچنان ۴ محاسبه شده است، در حالی که اختلاف میانگین‌ها بسیار پراکنده‌تر است.

در نهایت می‌بینیم که مربع کردن هر اختلاف و محاسبه جذر در آخر روش بهتری محسوب می‌شود.

 

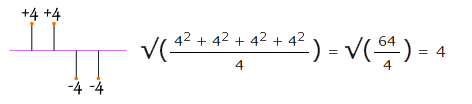
منبع : کانون علمی نخبگان شریف

مدل معادلات ساختاری از نوع تحلیل مسیر

در تحقیقاتی که هدف، آزمودن مدل خاصی از رابطه بین  متغیرها است، از تحلیل مدل معادلات ساختاری یا مدل های علّی استفاده می‌شود.

در این مدل داده ها به صورت ماتریس های کواریانس یا همبستگی درآمده و یک مجموعه معادلات رگرسیون بین متغیرها تدوین می‌شود. چنانچه در مدل برای هر متغیر از بیش از یک نشانگر استفاده شود، مدل شامل مولفه اندازه گیری نیز می‌شود.

تحلیل مدل معادلات ساختاری برآوردهایی از پارامترهای مدل (ضرایب مسیر و جملات خطا) و چند شاخص نیکویی برازش فراهم می آورد.

امکان تحلیل مدل های علّی پس از نگارش نرم افزارهایی از جمله لیزرل، آموس و smart PLS صورت گرفته است. این نرم افزارها به تدریج کامل تر و پیچیده تر شده اند.

مثالی از نمودار مسیر مدل ساختاری

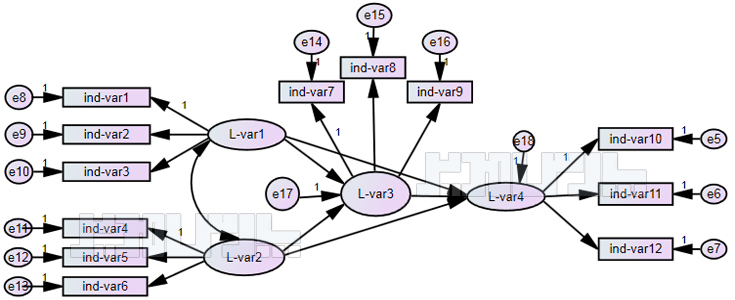
به طور کلی مدل های ساختاری به منظور بررسی اثرهای مستقیم و غیر مستقیم متغیرها در جهت شناخت روابط علی محتمل مورد استفاده قرار می گیرد. تصویر زیر یک نمونه نمودار تحلیل مسیر مدل ساختاری برآورد شده را نشان می دهد:

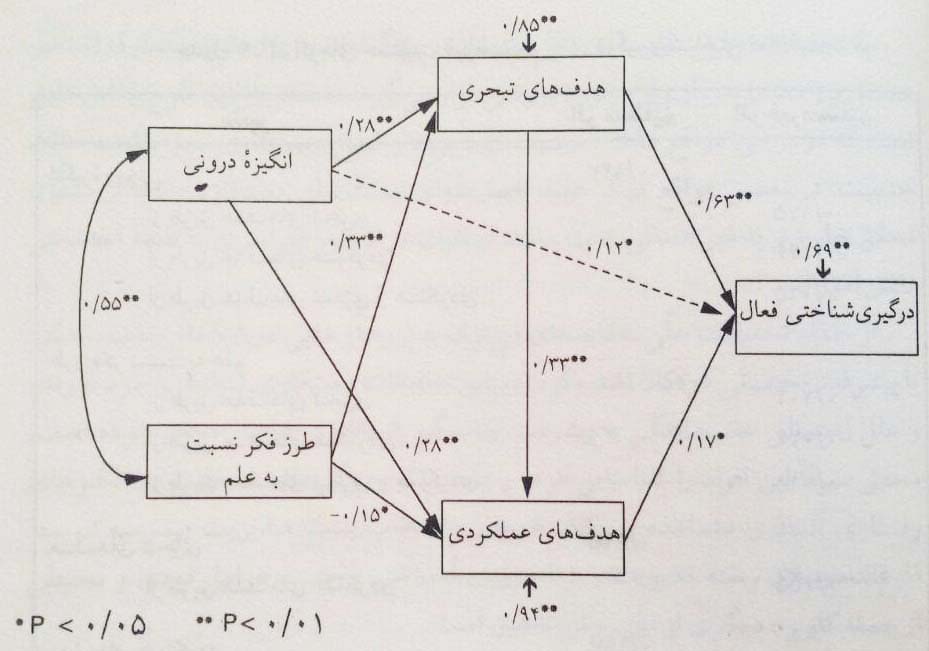
نمودار مسیر مدل ساختاری

 

منبع: داده پردازی آماری اطمینان شرق