آموزش تحلیل متغیر میانجی در مدل معادلات ساختاری

متاسفانه برایند اطلاعاتی که از کارهای محققین عزیز در کلاس های تحلیل آماری به ما می رسد این است که در آموزش تحلیل متغیر میانجی در مدل و حتی شناخت آن کج روی های بنیادی وجود دارد و حتی در بسیاری از رساله ها و مقاله ها این تحلیل با تحلیل متغیر های تعدیلگر خلط مبحث می شود. بنابراین بر آن شدیم که در قالب مقاله ای با زبان ساده آموزش تحلیل میانجی در مدل را مورد بحث قرار دهیم.

به روال آموزش های کلاس های مدلسازی معادلات ساختاری باید از پایه آغاز نمود و ابتدا برای محققین شرح داد متغیر میانجی چیست زیرا اکثر کج روی ها از شناخت این متغیر آغاز می گردد.

مطابق با تعریف بارون و کنی در سال ۱۹۸۶ متغیر میانجی یا mediator متغیری است که تمام یا بخشی از اثر متغیر مستقل بر وابسته را منوط به خود می کند. اشتباه دقیقا از عدم توجه به همین نکته شروع می شود. یعنی (تمام یا بخشی از اثر متغیر مستقل بر وابسته)، یعنی باید اثری بین این دو متغیر باشد که متغیر واسطه یا میانجی بتواند بخشی یا تمام آن را از خود عبور دهد(مرادی و میر الماسی، ۱۳۹۶)

فرض کنید در نقطه A  ظرف آبی قرار دارد که از لوله c به سمت B می رود. بنابراین ما مسیر آب در لوله مستقیم را داریم. حال می توان لوله ای فرعی کشید که آب ابتدا به مخزن M و بعد به مخزن B برود. دقیقا در مدل های ساختاری باید اثری از  متغیر A به سمت  B باشد که بعد متغیر میانجی M بتواند بخشی یا تمام اثر را از خود عبود دهد. بنابراین محققین عزیز در نظر داشته باشند که متغیر میانجی در شکل دوم قابل تحلیل است و شکل سوم تنها اثر غیر مستقیم بین A و B می باشد(مرادی و میر الماسی، ۱۳۹۶).

 

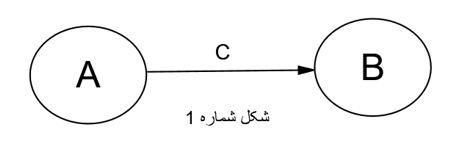
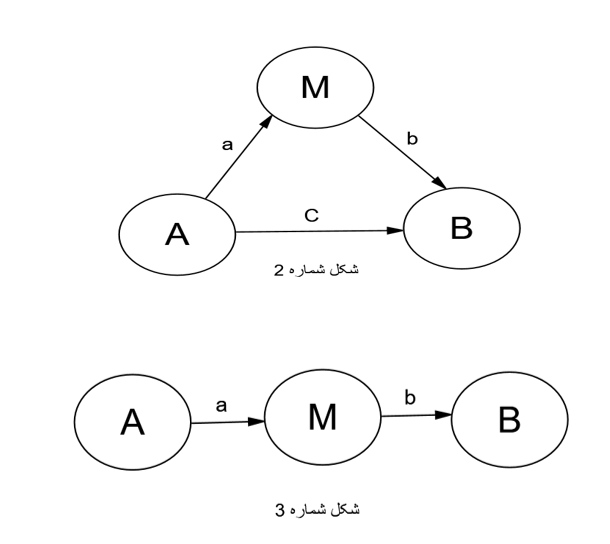
بنابراین برای تحلیل متغیر میانجی در مدل باید شکل مدل ساختاری پژوهش هم دارای مسیر مستقیم یعنی C و هم دارای مسیر غیر مستقیم یعنی  a×b  باشد. اکنون که می دانیم چه نوع متغیری قابلیت تحلیل میانجی را داراست به روش تحلیل و اجزای آن می رویم.

پیش از بیان تحلیل مسانجی باید گفت روش فرضیه نویسی از سال ۲۰۱۰ برای متغیر میانجی تغییر نموده است. زیرا با تفاق نظر صاحب نظران یک فرضیه باید با یک آزمون سنجش شود. یعنی وقتی به شکل ۴ نگاه میکنیم نمی توان با شیوه بسیار قدیمی بسیاری از اساتید تحلیل مسیر را انجام داد. مطابق با زنجیره گزاره های تحقیق آموزش داده شده در کلاس سه فلش تک جهته وجود دارد، بنابراین سه فرضیه نیز وجود دارد و نمیتوان آن را همانند موضوع تحقیق که کلی است و بنا بر آزمون در قالب فرضیه های مختلف است بررسی کرد. اگر بخواهم واضح تر بیان کنم برخی اساتید که با نرم افزار های آماری آشنایی کمتری دارند بیان می کنند که مثلا  متغیر مستقل بر متغیر وابسته با نقش میانجی گر M تاثیر می گذارد. این گزاره برای عنوان یک رساله میتواند قابل قبول و توجیه باشد اما برای یک فرضیه که تنها باید با یک آزمون سنجیده شود خیر. زیرا سه آزمون این سه مسیر را تخمین می زنند. بنابراین باید برای هر فلش یک فرضیه نوشت، سپس در نهایت پس از اجرای مدل در نرم افزار با انواع تحلیل های میانجی به بررسی متغیر میانجی پرداخت. (مرادی و میر الماسی، ۱۳۹۶)

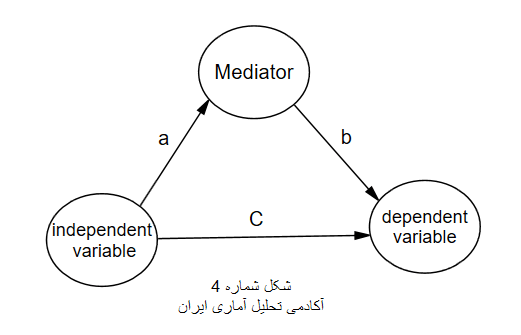
اکنون محقق باید بداند از تحلیل میانجی قرار است به چه اهدافی دست یابد. هدف از تحلیل میانجی این است که بدانیم متغیر میانجی ما:

• میانجی نیست: یعنی اثر متغیر مستقل بر وابسته را به خود منوط نمی کند.
• میانجی کامل است. یعنی تمام اثر متغیر مستقل بر وابسته را منوط به حضور خود می کند.
• میانجی جزیی است : یعنی بخشی از اثر متغیر مستقل بر وابسته را منوط به حضور خود می کند.

بنابراین برای رسیدن به این اهداف باید شاخص های زیر را بشناسد:

c : مسیر مستقیم یا اثر مستقیم نام دارد.

a×b : مسیر غیر مستقیم یا اثر غیر مستقیم  نام دارد.

 + c(a×b) : مسیر کل یا اثر کل نام دارد.

اما مهمترین شاخصی که باید بیاموزد variance accounted for(VAF) یا همان شمول واریانس است. شمول واریانس در حقیقت نسبت اثر غیر مستقیم بر اثر کل است. یعنی

VAF= (a×b) / (a×b)+c

اکنون باید بدانیم از چه رویکردی می خواهیم دست به تحلیل میانجی بزنیم.

دو رویکرد بارون و کنی و سوبل در کلاس های آکادمی تحلیل آماری ایران مورد بحث قرار گرفته است اما باید بیان کرد که رویکرد بوت استرپینگ با استفاده از نمونه گیری خودکار یعنی بوت استرپینگ به دلیل اینکه نرم افزار های مختلف مدل سازی معادلات ساختاری مثل ایموس و اسمارت پی ال اس از آن بهره می برند یکی از بهترین ها برای تحلیل میانجی محسوب می شود. البته رویکرد بوت استرپینگ پیش فرضی پیرامون شکل توزیع متغیر ها و نرمال بودن آن ها ندارد و برای حجم نمونه های کوچک با اطمینان بیشتری می تواند بکار رود. اما باید بیان کرد که در زمانی که متغیر میانجی در مدل حضور ندارد باید مسیر مستقیم و اثر آن از نظر آماری معنادار باشد(ژائو و همکاران، ۲۰۱۰)

بنابراین باید یکبار مدل را بدون حضور میانجی و بار دیگر با حضور متغیر میانجی در نرم افزار اجرا نماییم و از الگوریتم زیر پیروی کنیم

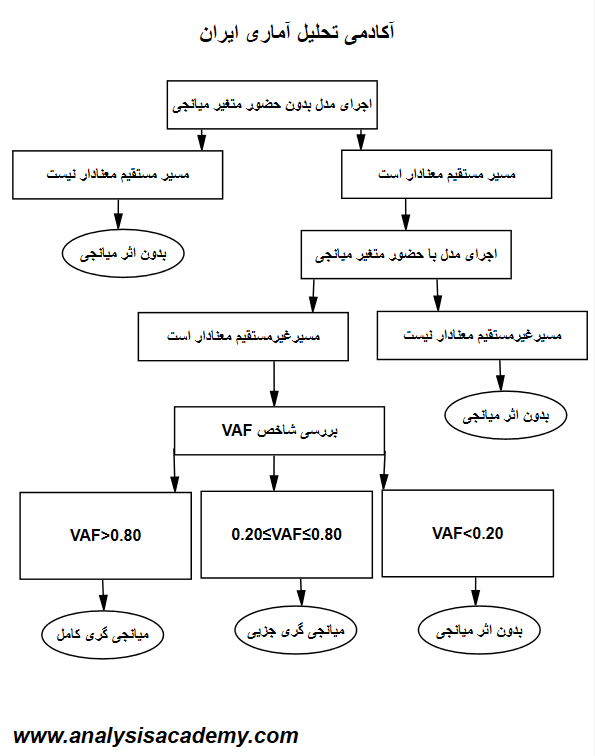
مشخص است که اگر مسیر غیر مستقیم معنادار باشد که به معنای این است که هم a و b معنادار است که حاصلضرب آن ها نیز معنادار است می توان به ارزیابی VAF پرداخت و در یکی از حالت های سه گانه الگوریتم قرار گرفت. اما نباید فراموش کرد که حالت استثنایی را نیز پرفسور هایر در مطالعات خود بیان می کند. و آن زمانی است که با ورود متغیر میانجی به مدل در مدل دوم اجرایی محقق رابطه علی مسیر مستقیم تغییر جهت می دهد. یعنی مثلا قبل از ورود میانجی رابطه علی مثبت و معنادار است اما بعد از ورود آن به مدل رابطه آن ها منفی و معنادار می شود. این پدیده را suppressor effect  یا اثر سرکوبگر می خوانند که می تواند مقدار VAF را بزرگتر از یک نماید. در آن صورت دیگر آزمون دارای پاسخ کاذب بوده و قابل تفسیر نیست(مرادی، میر الماسی، ۱۳۹۶)

محسن مرادی