آمار پارامتری و ناپارامتری

در تحلیل‌های آماری بخصوص مباحث مربوط به آزمون‌های فرض آماری، بر وجود توزیع برای داده‌ها تکیه داریم. در این حالت برای داده‌های کمی، «توزیع نرمال» (Normal Distribution) و برای داده‌های کیفی، توزیع «دوجمله‌ای» (Binomial Distribution) یا «چند جمله‌ای» (Multinomial) در نظر گرفته می‌شود. به این ترتیب هنگام استفاده از روش‌های آماری هرچه قیدهای بیشتری در مورد توزیع داده‌ها داشته باشیم به «روش‌های پارامتری» (Parametric Methods) نزدیک‌تر شده‌ایم. مشخصا این شیوه و روش‌ها در «آمار پارامتری» (Parametric Statistics) مورد بحث و بررسی قرار می‌گیرند. برعکس هر چه قیدهای کمتری در مورد توزیع داده‌ها وجود داشته باشد، روش‌های تحلیلی به سمت «روش‌های ناپارامتری» (Non-Parametric methods) می‌روند و به شاخه «آمار ناپارامتری» (Non-Parametric Statistics) نزدیک می‌شوند. این نوشتار به آمار پارامتری و ناپارامتری اختصاص داشته و ویژگی و خصوصیات هر یک را بازگو می‌کند.

 

در این نوشتار به بررسی تفاوت روش‌های پارامتری و ناپارامتری در آمار می‌پردازیم و نقاط ضعف و قوت هر یک را مرور خواهیم کرد. برای مطالعه بیشتر در زمینه تحلیل‌ها و آزمون‌های فرض آماری مطلب آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات مناسب به نظر می‌رسد. همچنین آگاهی از نحوه اجرای آزمون‌های پارامتری در مورد میانگین جامعه که در نوشتار آزمون فرض میانگین جامعه در آمار — به زبان ساده آمده است، خالی از لطف نیست.

آمار پارامتری و ناپارامتری

در حوزه «تجزیه و تحلیل آماری داده‌ها» (Statistical Data Analysis)، توزیع جامعه آماری که نمونه از آن گرفته شده، مهم است زیرا هر چه اطلاعات بیشتر در زمینه رفتار داده‌ها و شکل پراکندگی و توزیع آن‌ها وجود داشته باشد، نتایج قابل اعتمادتر و دقیق‌تر خواهند بود. در مقابل، وجود اطلاعات کم از توزیع جامعه آماری مربوط به نمونه، باعث کاهش اعتماد به نتایج حاصل از روش‌های معمول (پارامتری) آماری می‌شود. بنابراین در این حالت مجبور به استفاده از روش‌های ناپارامتری هستیم که برای اجرای آن‌ها فرضیاتی در مورد توزیع داده‌ها وجود ندارد. به همین علت به روش‌های ناپارامتری گاهی «روش‌های توزیع-آزاد» (Distribution-free Methods) نیز می‌گویند.

آمار پارامتری و روش‌های تجزیه و تحلیل مرتبط

داده‌های پارامتری به نمونه‌ای گفته می‌شود که از توزیع جامعه آماری آن مطلع هستیم. معمولا این توزیع آماری برای داده‌های کمی، نرمال یک یا چند متغیره در نظر گرفته می‌شود. در این حالت از آزمون‌های آماری پارامتری مثل آزمون T، آزمون F و یا آزمون Z استفاده می‌کنیم. همچنین برای اندازه‌گیری میزان همبستگی بین متغیرهای دو یا چند بعدی نیز از ضریب همبستگی پیرسون استفاده خواهیم کرد.

 

اگر حجم نمونه در روش‌های تجزیه و تحلیل آمار پارامتری بزرگ انتخاب شود، معمولا توان آزمون مناسب خواهد بود و به راحتی می‌توان نتایج حاصل از آزمون فرض را به جامعه نسبت داد. جدول زیر به معرفی روش‌های پارامتری در انجام آزمون‌های فرض آماری پرداخته است.

مسئله	نوع آزمون	شرایط اجرای آزمون
مقایسه میانگین با مقدار ثابت از جامعه نرمال با واریانس معلوم	آزمون تک نمونه‌ای با آماره Z	مشاهدات بیشتر از 30 نمونه و چولگی نیز کم باشد.
مقایسه میانگین با مقدار ثابت از جامعه نرمال با واریانس نامعلوم	آزمون تک نمونه‌ای با آماره T	مشاهدات بیشتر از 20 نمونه و چولگی نیز کم باشد.
مقایسه میانگین دو جامعه مستقل نرمال با واریانس معلوم	آزمون دو نمونه‌ای با آماره Z	در هر گروه تعداد مشاهدات بیشتر از ۳۰ باشد و چولگی نیز کم باشد.
مقایسه میانگین دو جامعه مستقل نرمال با واریانس نامعلوم	آزمون دو نمونه‌ای با آماره T	در هر گروه تعداد مشاهدات بیشتر از 20 باشد و چولگی نیز کم باشد.
مقایسه میانگین زوجی	آزمون دو نمونه‌ای زوجی با آماره T	مشاهدات زوجی بیش از ۲۰ مشاهده باشند، چولگی نیز کم باشد.
مقایسه میانگین چند جامعه مستقل نرمال با واریانس برابر ولی نامعلوم	آنالیز واریانس (ANOVA)	تعداد مشاهدات نمونه در هر گروه از جامعه بیش از ۲۰ باشد. واریانس‌ها برابر یا تقریبا برابر باشند، هر جامعه دارای توزیع نرمال باشد.
…	…	…

آمار ناپارامتری و روش‌های تجزیه و تحلیل مرتبط

اگر توزیع جامعه آماری نامشخص باشد و از طرفی حجم نمونه نیز کوچک باشد بطوری که نتوان از قضیه حد مرکزی برای تعیین توزیع حدی یا مجانبی جامعه آماری، استفاده کرد، از تحلیل‌های ناپارامتری استفاده می‌شود، زیرا در این حالت کارآمدتر از روش‌های پارامتری هستند. به این ترتیب در زمانی که توزیع جامعه مشخص نباشد و یا حجم نمونه کم باشد، روش‌ها و آزمون‌های ناپارامتری نسبت به روش‌ها و آزمون‌های پارامتری از توان آزمون بیشتری برخوردارند و نسبت به آن‌ها ارجح هستند.

بهتر است شرایط بهره‌گیری از روش‌های ناپارامتری را به صورت زیر لیست کنیم:

• برای داده‌ها، نتوان توزیع آماری مناسبی در نظر گرفت.
• وجود داده‌های پرت (Outlier)، وجود چند نما و … امکان انتخاب توزیع نرمال را برایشان میسر نمی‌کند.
• کم بودن حجم نمونه برآورد پارامترهای توزیع نرمال مانند میانگین و بخصوص واریانس را دچار مشکل می‌کند و در عمل امکان بررسی توزیع نرمال به علت حجم کم نمونه برای جامعه وجود ندارد.

روش‌های ناپارامتری در چنین موقعیت‌های می‌تواند راهگشا باشد و به محقق و «تحلیل‌گر داده‌» (Data Scientist) برای شناخت داده‌ها یاری برساند.

نکته: باید توجه داشت که اگر توزیع جامعه آماری قابل تحقیق و تعیین باشد، اجرای روش‌های پارامتری بر روش‌های ناپارامتری ارجح هستند زیرا در این حالت روش‌های پارامتری نسبت به روش‌های ناپارامتری از دقت بیشتری برخوردارند. بنابراین فقط زمانی که از توزیع جامعه آماری مطلع نیستم، به اجبار از روش‌های ناپارامتری استفاده خواهیم کرد. البته اگر حجم نمونه بزرگ باشد، در اکثر موارد، نتایج حاصل از آزمون‌های پارامتری و ناپارامتری با یکدیگر همخوانی دارند.

 

از آنجایی که در بیشتر روش‌های ناپارامتری به جای داده‌ها، ترتیب آن‌ها به کار گرفته می‌شود، بهتر است با مفهوم رتبه‌ (Rank) بیشتر آشنا شویم. در ادامه به معرفی رتبه و کاربردهای آن در آمار ناپارامتری می‌پردازیم.

داده‌های رتبه‌بندی شده (Ranked Data)

استفاده از رتبه‌ها به جای مقدارها، یکی از ویژگی‌های روش‌های ناپارامتری است. برای مثال همانطور که دیده‌اید ضریب همبستگی اسپیرمن یک روش ناپارامتری برای اندازه‌گیری همبستگی بین مقدارها است. برای محاسبه ضریب همبستگی اسپیرمن به جای استفاده از مقدارها، رتبه‌هایشان ملاک قرار می‌گیرد و ضریب همبستگی عادی (پیرسون) به جای مقدارها از روی رتبه‌ها محاسبه می‌شود.

برای ایجاد رتبه‌ها کافی است که آن‌ها را به ترتیب چیده و از کمترین تا بیشترین مقدار، برچسب‌های از ۱ تا N را نسبت دهیم. این برچسب‌ها «رتبه‌» (Rank) را نشان می‌دهد.

برای مثال فرض کنید که ۵ مقدار مختلف در یک ستون داریم.

 

1 2 3 4 5

0.020 0.184 0.431 0.550 0.620

اگر آن‌ها را مرتب و رتبه‌بندی کنیم، به صورت زیر قرار خواهند گرفت. همانطور که دیده می‌شود، کوچکترین مقدار، رتبه ۱ و بزرگترین مقدار نیز رتبه 5 گرفته است.

 

1 2 3 4 5

1 = 0.021055 2 = 0.404622 3 = 0.488733 4 = 0.618510 5 = 0.832803

اگر منظور مقایسه بین دو جامعه باشد، می‌توان برای نمونه دوم نیز به همین ترتیب عمل کرد و بین رتبه‌های حاصل، مقایسه انجام داد.

نکته: اگر در بین داده‌های موجود در نمونه، دو مقدار یا بیشتر با یکدیگر برابر باشند، ممکن است برای دو مقدار یکسان شیوه‌های رتبه‌بندی متفاوتی به کار گرفته شود. برای مثال ممکن است حداقل یا حداکثر رتبه انتخاب شود. حتی میانگین رتبه‌ها نیز یکی از روش‌های تخصیص رتبه است.

در زیر کد مربوط به رتبه‌بندی داده‌ها به زبان پایتون نوشته شده است. در اینجا ۱۰۰۰ عدد تصادفی تولید شده و پس از رتبه‌بندی، ۱۰ سطر اول نمایش داده شده‌اند.

 

1 2 3 4 5 6 7 8 9 10 11 12 13

from numpy.random import rand from numpy.random import seed from scipy.stats import rankdata # seed random number generator seed(1) # generate dataset data = rand(1000) # review first 10 samples print(data[:10]) # rank data ranked = rankdata(data) # review first 10 ranked samples print(ranked[:10])

نتیجه اجرای این کد به صورت زیر خواهد بود.

 

1 2 3 4

[4.17022005e-01 7.20324493e-01 1.14374817e-04 3.02332573e-01 1.46755891e-01 9.23385948e-02 1.86260211e-01 3.45560727e-01 3.96767474e-01 5.38816734e-01] [408. 721.   1. 300. 151.  93. 186. 342. 385. 535.]

همانطور که گفته شد، گاهی ممکن است بعضی از مقدارها در لیست داده‌ها با هم برابر باشند. در این میان رتبه‌ها برایشان یکسان خواهد بود. چنین موقعیتی را «گره» (Tie) می‌نامند. برای آنکه با شیوه‌های مختلف رتبه و ایجاد گره‌ها آشنا شوید کد زیر در R تهیه شده است. همانطور که مشخص است اعداد ۱ تا ۵ لیست شده‌اند ولی عدد ۳ دوبار تکرار شده است. انتظار داریم که برای این شش عدد رتبه‌های مختلفی ایجاد شود.

 

1 2 3 4 5 6 7 8

x=c(1,2,3,3,4,5) method= c("min","max","average","random","first") for (i in method)   { r=rank(x,ties.method =i) print(paste(" method = ",i)) print(r) }

خروجی به صورت زیر خواهد بود.

 

1 2 3 4 5 6 7 8 9 10 11

[1] " method =  min" [1] 1 2 3 3 5 6 [1] " method =  max" [1] 1 2 4 4 5 6 [1] " method =  average" [1] 1.0 2.0 3.5 3.5 5.0 6.0 [1] " method =  random" [1] 1 2 4 3 5 6 [1] " method =  first" [1] 1 2 3 4 5 6 >

همانطور که دیده می‌شود ۵ روش معمول برای مشخص کردن رتبه برای گره‌ها وجود دارد. در روش Min، کمترین رتبه برای مقدارهای تکراری در نظر گرفته می‌شود. همچنین به کمک روش Max، بزرگترین رتبه را برای داده‌های تکراری قرار خواهیم داد. روش میانگین یا Average یکی از معمول‌ترین روش‌ها است که میانگین رتبه‌ها را برای مقدارهای تکراری در نظر می‌گیرد. روش‌های تصادفی یا Random نیز از رتبه‌های ایجاد شده برای هر داده‌ تکراری، یکی را به تصادف انتخاب و به آن نسبت می‌دهد. همچنین در روش اول یا First، مشاهدات به ترتیب رتبه بندی شده و رتبه تکراری نخواهیم داشت.

نکته: در روش‌های Min, Max و Average، رتبه برای داده‌های تکراری، یکسان خواهد بود ولی در روش Random و First هر مشاهده رتبه منحصر به فردی خواهد داشت.

انواع روش‌های آزمون‌های ناپارامتری

روش‌های آزمون فرض آمار ناپارامتری که وابسته به رتبه‌ها هستند در جدول زیر معرفی شده‌اند.

مسئله	نوع آزمون
آزمون تک نمونه‌ای- مقایسه میانگین با مقدار ثابت	آزمون علامت (Sign test) آزمون ویلکاکسون (Wilcoxon)
آزمون دو نمونه‌ای مستقل	آزمون من ویتنی (Mann-Whitney)
آزمون مقایسه میانگین چند جامعه مستقل	آزمون کروسکال والیس (Kruskal-Wallis) آزمون میانه (Mood’s median test)
آنالیز واریانس دو طرفه	آزمون فریدمن (Friedman test)

از آنجایی در زمان وجود چولگی زیاد در داده‌ها، «میانه» (Median) معیار مرکزی مناسب‌تری نسبت به میانگین است، در بسیاری از تحلیل‌های ناپارامتری میانه محاسبه و مقایسه می‌شود. بنابراین زمانی که میانه برآوردگر بهتری برای نقطه تمرکز جامعه آماری باشد، روش‌های ناپارامتری مفید خواهند بود.

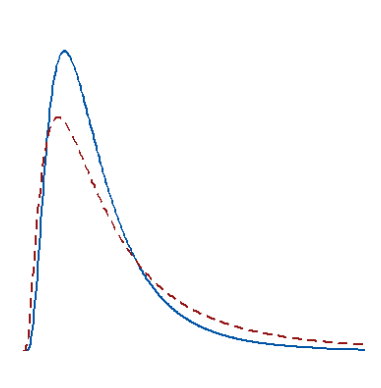
از طرف دیگر وجود داده‌های پرت نیز باعث انحراف میانگین خواهند شد. در چنین مواقعی باز هم میانگین نمی‌توان نماینده خوبی برای مشاهدات باشد. در چنین مواقعی نیز از میانه استفاده شده و به کارگیری روش‌های ناپارامتری مفید و موثرتر از روش‌های پارامتری است.

در روش‌های ناپارامتری علاوه بر رتبه‌ها از چندک‌ها (چارک، دهک و صدک) نیز به کار گرفته می‌شوند. روش‌های «رگرسیون ناپارامتری» (Non Parametric Regression) بر چنین شاخص‌های تکیه دارند.

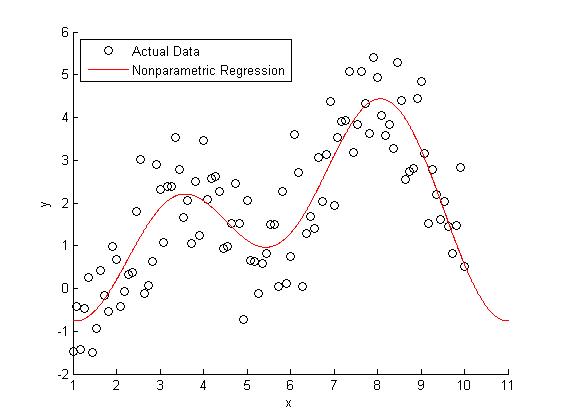
در نوشتارهای آینده به بررسی روش‌های آمار ناپارامتری نظیر «رگرسیون چندکی» (Quantile Regression) و همچنین «آزمون‌های فرض ناپارامتری» (Nonparametric Hypothesis Tests) خواهیم پرداخت. همچنین در آنجا برای انجام محاسبات مربوط به این گونه روش‌ها از نرم‌افزارهای آماری نظیر SPSS، Minitab و R نیز کمک خواهیم گرفت.

منبع: https://blog.faradars.org/parametric-and-non-parametric-statistics/