شرایط و پیش فرض های تحلیل کوواریانس (آنکووا) ANCOVA

هدف از انجام تحلیل کوواریانس

هدف از انجام تحلیل کوواریانس (ANCOVA) در مطالعات کار آزمایی بالینی مقایسه دو گروه کیس و کنترل بعد از مداخله (پس آزمون) با یکدیگر است. در صورتی که اندازه های قبلی (پیش آزمون) کنترل شده باشد. در نهایت تحلیل کوواریانس به این سوال پاسخ می دهد که آیا مداخله موثر و معنی دار بوده است یا خیر ؟

در واقع یکی از راه های کنترل اثرات نمره پیش آزمون به عنوان اثر انتقال، استفاده از آزمون آنالیز کوواریانس (ANCOVA) است. به طوری که شرایطی برای مطالعه فراهم می شود. تا اثرات درمان را جدا از اثر بالقوه نمره پیش آزمون بررسی کند.

تفاوت تحلیل کوواریانس (ANCOVA) و تحلیل واریانس (ANOVA)

آنکووا گسترش داده شده ی آنالیز واریانس است که پیش فرض های آن را نیز دارد. تفاوت آشکار بین ANOVA و ANCOVA حرف “C” است که مخفف “کواریانس” است. مانند ANOVA، “تجزیه و تحلیل کوواریانس” (ANCOVA) یک متغیر پاسخ پیوسته دارد. تحلیل کوواریانس (ANCOVA) مانند تحلیل واریانس برای تشخیص تفاوت در میانگین چند گروه متغیر مستقل، در حالی که کار کنترل متغیرهای کووریت (Covariate Variables) را انجام می دهد، استفاده می شود. متغیر کووریت معمولاً جزئی از سؤال اصلی تحقیق نیست اما می تواند متغیر وابسته را تحت تأثیر قرار دهد و بنابراین باید کنترل شود.

در حالی که آنالیز واریانس به دنبال اختلاف در بین میانگین ها است. تحلیل کوواریانس به دنبال اختلاف میانگین های تعدیل شده (به وسیله متغیر کووریت که به آن متغیر مخدوش کننده نیز می گویند) می باشد.

پیش فرض های تحلیل کوواریانس تک متغیره (ANCOVA)

قبل از معرفی پیش فرض های تحلیل کوواریانس، از این که یک یا چند پیش فرض معرفی شده در هنگام آنالیز دیتا با نرم افزار SPSS رعایت نشود تعجب نکنید ! همیشه داده استخراج شده از دنیای واقعی مانند مثال های موجود در متن کتاب ها همه چیز را مطلوب نشان نمی دهد. همچنین از این که چند پیش فرض اصلی هم رد شود نگران نشوید ! همیشه یک راه حلی باید وجود داشته باشد.

پیش فرض اول : پیوسته بودن متغیر وابسته و کووریت

متغیر وابسته و متغیر کووریت بایستی پیوسته باشد. برای مثال متغیر زمان (که با واحد ساعت اندازه گیری می شود)، نمرات IQ (امتیاز IQ) نمرات امتحان (0 تا 20) و وزن (به کیلوگرم) پیوسته و کمی می باشد. البته متغیرهای کووریت (متغیرهای مخدوش کننده) می تواند رسته ای نیز باشد (مانند جنسیت). که در این حالت آزمون ANCOVA ترجیح داده نمی شود.

پیش فرض دوم : رسته ای بودن متغیر مستقل

متغیر مستقل بایستی شامل دو یا چند سطح باشد برای مثال جنسیت که دارای دو سطح زن و مرد است. همچنین متغیر گروه تحقیق که شامل (گروه کیس و گروه کنترل) است. فعالیت فیزیکی (کم، متوسط، زیاد) نیز مثال دیگری از این قبیل می باشد.

پیش فرض سوم : استقلال مشاهدات

هیچ ارتباطی بین مشاهدات در هر گروه و یا بین گروه ها وجود نداشته باشد. همچنین هیچ یک از شرکت کننده ها (اعضای نمونه) در بیش از یک گروه نباشد. البته این موضوع بیشتر به طراحی مطالعه مربوط می شود. اگر این پیش فرض رعایت نشود نیاز به یک آزمون آماری دیگری به جای آزمون ANCOVA می باشد.

پیش فرض چهارم : عدم وجود داده پرت

در بین داده های پژوهش نباید داده پرت قابل توجهی وجود داشته باشد. چرا که وجود داده پرت ممکن است بر نتایج بدست آمده از تحلیل کوواریانس تاثیر منفی بگذارد و از اعتبار نتایج آن کاهش دهد.

پیش فرض پنجم : نرمال بودن باقی مانده ها

برای هر سطح از متغیر مستقل، باقی مانده بدست آمده تقریبا بایستی دارای توزیع نرمال باشد. به این دلیل از واژه تقریبا استفاده کردیم چون می دانیم این پیش فرض در اکثر اوقات اتفاق نمی افتد در حالی که نتایج بدست آمده از تحلیل کوواریانس معتبر باقی می ماند.

پیش فرض ششم : همگنی واریانس ها

این پیش فرض به کمک انجام آزمون لون (Levene’s test) در نرم افزار SPSS قابل بررسی است.

پیش فرض هفتم : ارتباط خطی کووریت با متغیر وابسته

در هر سطح از متغیر مستقل، متغیر کووریت رابطه خطی با متغیر وابسته دارد. این پیش فرض به کمک نرم افزار SPSS از طریق رسم Scatter plot گروه بندی شده از متغیر کووریت، پیش آزمون متغیر وابسته و متغیر مستقل بررسی می شود.

پیش فرض هشتم : همسانی واریانس

این پیش فرض به کمک نرم افزار SPSS از طریق رسم Scatter plot ار باقی مانده های رگرسیون در مقابل مقادیر پیش بینی شده بررسی می شود.

پیش فرض نهم : همگنی شیب رگرسیون

 همگنی شیب رگرسیون بدین معنی است که شیب رگرسیونی خطوط مختلف در بین گروه ها باید برابر باشد. به عبارت دیگر تعامل نمرات کووریت و متغیر مستقل در بین گروه ها نباید اختلاف معنی داری داشته باشد. به عبارتی دیگر، نیاز هست که شیب های خطوط رگرسیونی برای کووریت ها (در ارتباط با متغیر وابسته) در بین گروه ها (کیس و کنترل) یکسان باشد که به این پیش فرض همگنی شیب رگرسیون گفته می شود که می تواند با یک آزمون F بر روی تعامل متغیرهای مستقل با کووریت ها ارزیابی شود. اگر آزمون F معنادار بود، بدین معنی است که این پیش فرض نقض شده است.

ارائه مثال انجام تحلیل کوواریانس در SPSS

در یک مطالعه ای فرضی، پرسشنامه کیفیت زندگی در اختیار 60 نفر از مبتلایان به صرع شرکت کننده در پژوهش قرار داده شد تا آن را تکمیل نمایند. این 60 نفر به صورت تصادفی به دو گروه 30 (کنترل) و 30 (کیس) تقسیم بندی شدند. بیماران گروه کیس (Case) تحت مداخله (پیگیری تلفنی به صورت برقراری 10 تماس 15 دقیقه ای) در طی دو ماه قرار گرفتند. همچنین، در بیماران گروه کنترل (Control) هیچ گونه مداخله ای انجام نشده و آموزش های روتین را دریافت کردند. پس از دو ماه و حین مراجعه به درمانگاه، کیفیت زندگی در دو گروه کیس و کنترل مجددا مورد بررسی قرار گرفت.

 

نحوه ورود داده برای انجام تحلیل کوواریانس در SPSS

برای سادگی نمایش داده های وارد شده، فقط نمرات کل کیفیت زندگی را قبل و بعد از مداخله مانند شکل زیر در نرم افزار SPSS وارد کرده‌ایم. توجه داشته باشید که نمرات گروه کیس و کنترل در پیش آزمون و پس آزمون بایستی در یک ستون و زیر هم وارد نرم افزار شود و با ایجاد متغیر دو سطحی گروه تحقیق از لحاظ گروه مطالعه قابل تشخیص باشد.

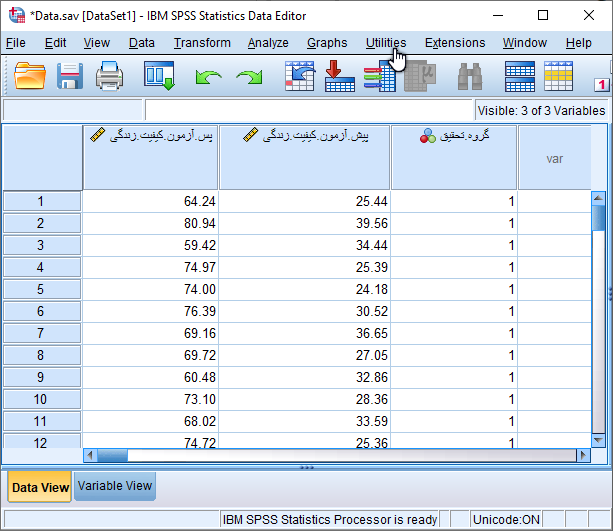
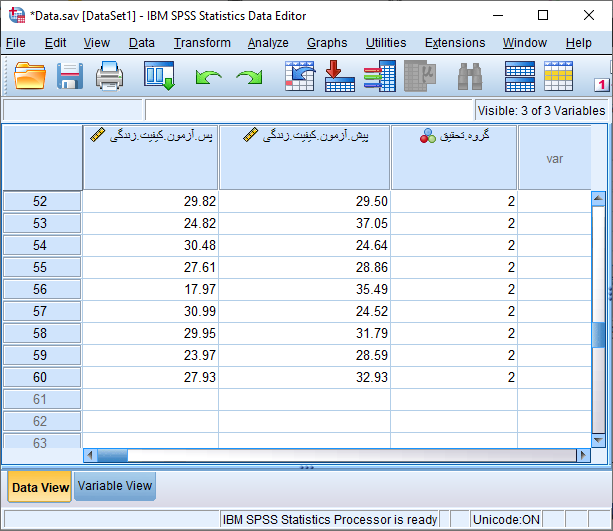
حال دیتا برای انجام آزمون تحلیل کوواریانس آماده شده است. از طریق مسیر زیر در نرم افزار SPSS آزمون ANCOVA را انجام می دهیم.

Analyze / General Linear Model / Univariate

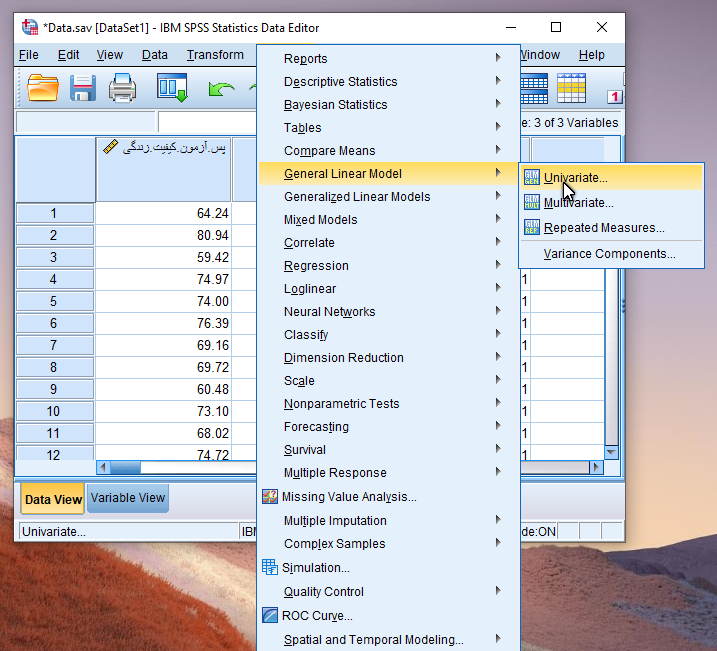
پس از انجام مسیر فوق پنجره زیر جهت تنظیمات تحلیل کوواریانس قابل مشاهده است.

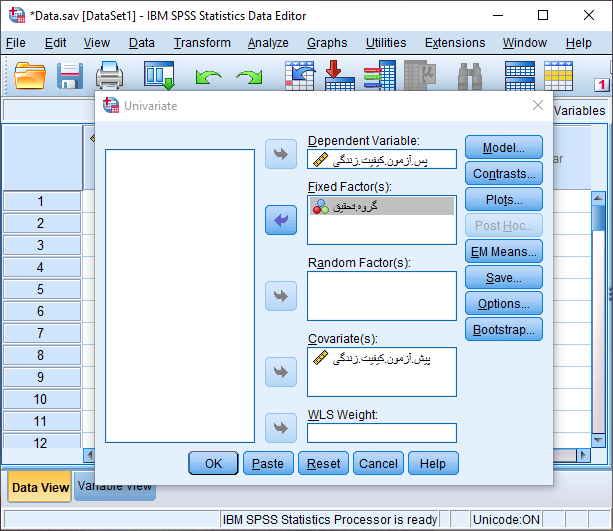
همانند شکل فوق، متغیر کیفیت زندگی پس از مداخله (پس آزمون) را به عنوان متغیر وابسته در کادر Dependent Variable، متغیر کیفیت زندگی قبل از مداخله (پیش آزمون) را به عنوان متغیر کووریت (مخدوش کننده) در کادر Covariate(s) و متغیر گروه را در کادر Fixed Factor(s) به عنوان متغیر مستقل وارد می کنیم. ابتدا برای بررسی پیش فرض همگنی شیب رگرسیونی از طریق دکمه Moldel پنجره زیر را باز می کنیم.

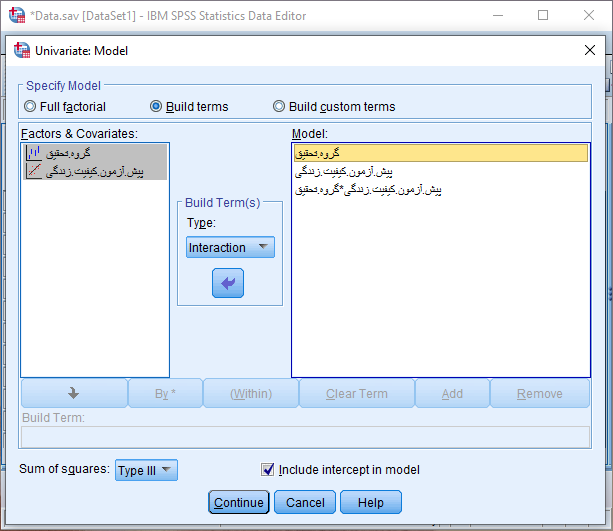
مانند شکل فوق ابتدا در کادر Specify Model گزینه Build terms را فعال می‌کنیم. سپس در کادر Model متغیرهای (گروه تحقیق، پیش آزمون و متغیر ضربی پیش آزمون کیفیت زندگی * گروه تحقیق را وارد می کنیم. با کلیک بر روی دکمه Continue مجدد وارد پنجره قبلی می شویم. حال با کلیک بر روی دکمه OK خروجی نرم افزار به صورت زیر مشاهده می شود.

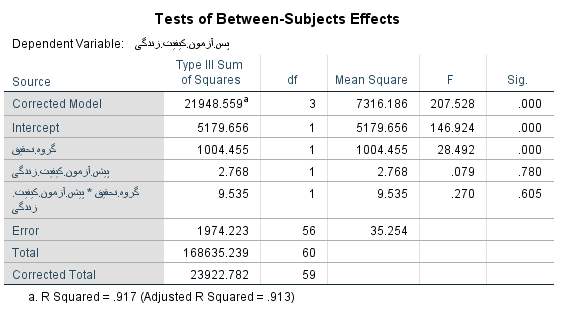
با توجه به جدول فوق ملاحظه می شود سطح معنی داری متغیر گروه تحقیق*پیش آزمون کیفیت زندگی برابر 0.605 و بیشتر از 0.05 می باشد. این امر نشان دهنده این است که پیش فرض همگنی شیب رگرسیون رعایت می شود.

حال برای بررسی پیش فرض همگنی واریانس ها از طریق دکمه Moldel پنجره زیر را باز کرده و مانند شکل زیر تنظیمات لازمه را انجام می دهیم.

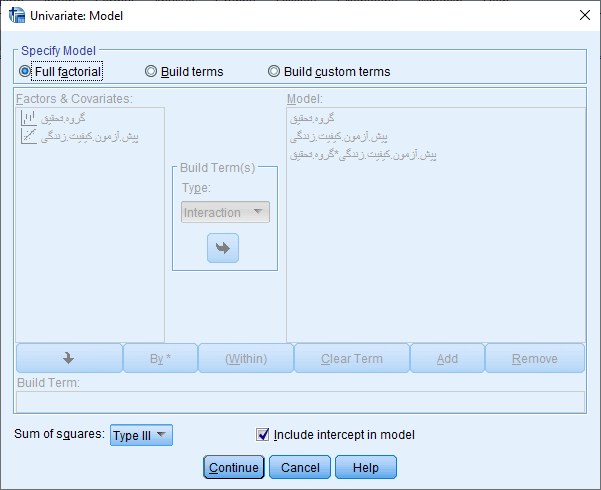
مانند شکل فوق ابتدا در کادر Specify Model گزینه Full factorial را فعال می‌کنیم. با کلیک بر روی دکمه Continue مجدد وارد پنجره قبلی می شویم.

در این پنجره از طریق گزینه Options پنجره زیر باز می شود.

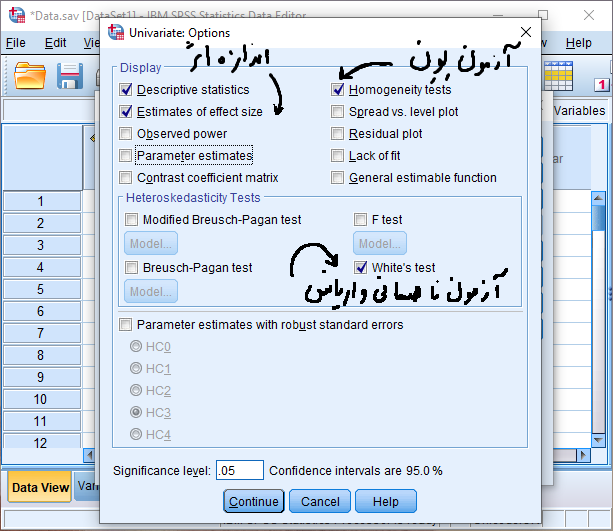
پس از انجام تنظیمات فوق با کلیک بر روی دکمه Continue مجدد وارد پنجره قبلی می شویم. حال با کلیک بر روی دکمه OK خروجی نرم افزار به صورت زیر مشاهده می شود.

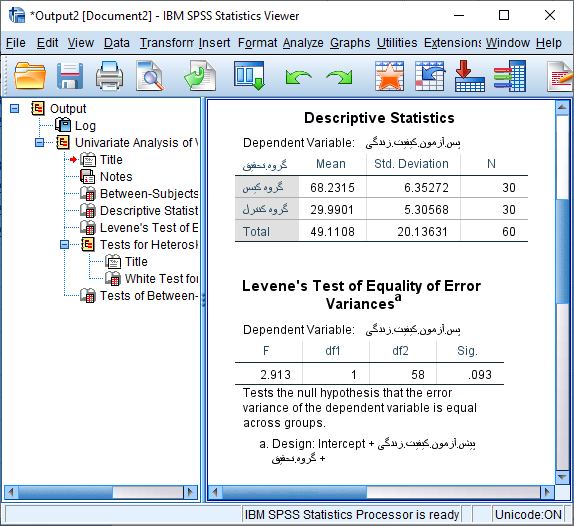
با توجه به سطح معنی ­داری شکل فوق (0.093) فرضیه صفر مبنی بر همگونی واریانس ­ها در دو گروه شاهد و آزمایش در سطح 5 درصد رد نمی­ گردد. در نتیجه فرضیه برابری واریانس ­ها تایید می ­شود.

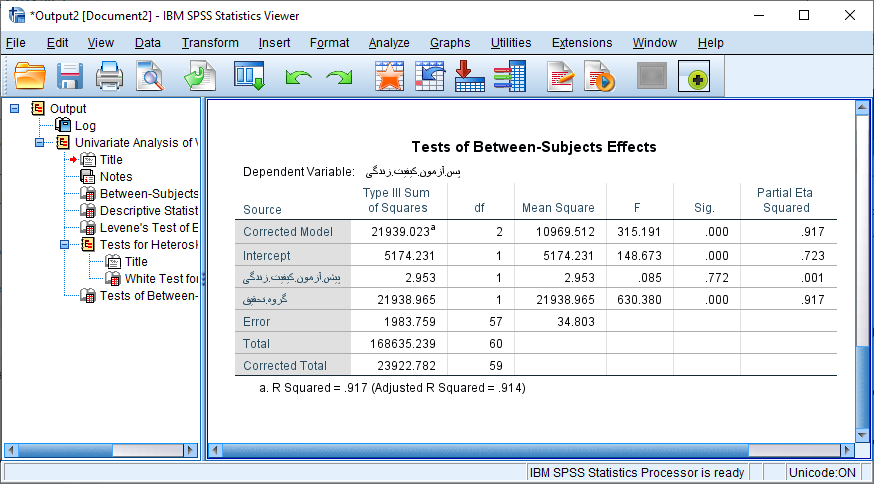
در جدول فوق فوق ملاحظه می­ شود، در پس آزمون نمرات کیفیت زندگی کل آزمایش (گروهی که پیگیری تلفنی دریافت کردند) با نمرات کیفیت زندگی در گروه گواه تفاوت معنی داری وجود دارد (سطح معنی داری کمتر از 0.05). در نتیجه می­ توان دریافت که بیمارانی که مداخله دریافت می­ کنند، نسبت به دیگر افراد، کیفیت زندگی کل بیشتری دارند. به طور کلی مشاهدات بیان می­ کند که پیگیری تلفنی بر بهبود کیفیت زندگی افراد با اندازه اثر (0.917) تاثیر گذار است.

 

منبع: https://cochrana.ir