شاخه های مختلف علوم برای تجزیه و تحلیل داده ها از روش های مختلفی مانند روش های ذیل استفاده می نمایند:
الف) روش تحلیل محتوا
ب) روش تحلیل آماری
ج) روش تحلیل ریاضی
د) روش اقتصاد سنجی
ه) روش ارزشیابی اقتصادی
و) ...
تمرکز این نوشتار بر روش های تجزیه و تحلیل سیستمهای اقتصادی اجتماعی و بویژه روش های تحلیل آماری می باشد.
آمار علم طبقه بندی اطلاعات، علم تصمیم گیری های علمی و منطقی، علم برنامه ریزی های دقیق و علم توصیف و بیان آن چیزی است که از مشاهدات می توان فهمید.
هدف ما آموزش درس آمار نیست زیرا اینگونه مطالب تخصصی را میتوان در مراجع مختلف یافت، هدف اصلی ما ارائه یک روش دستیابی سریع به بهترین روش آماری می باشد.
یکی از مشکلات عمومی در تحقبقات میدانی انتخاب روش تحلیل آماری مناسب و یا به عبارتی انتخاب آزمون آماری مناسب برای بررسی سوالات یا فرضیات تحقیق می باشد.
در آزمون های آماری هدف تعیین این موضوع است که آیا داده های نمونه شواهد کافی برای رد یک حدس یا فرضیه را دارند یا خیر؟
انتخاب نادرست آزمون آماری موجب خدشه دار شدن نتایج تحقیق می شود.
دکتر غلامرضا جندقی استاد یار دانشگاه تهران در مقاله ای کاربرد انواع آزمون های آماری را با توجه به نوع داده ها و وبژگی های نمونه آماری و نوع تحلیل نشان داده است که در این بخش به نکات کلیدی آن اشاره می شود:
قبل از انتخاب یک آزمون آماری بایستی به سوالات زیر پاسخ داد:
1- چه تعداد متغیر مورد بررسی قرار می گیرد؟
2- چند گروه مفایسه می شوند؟
3- آیا توزیع ویژگی مورد بررسی در جامعه نرمال است؟
4- آیا گروه های مورد بررسی مستقل هستند؟
5- سوال یا فرضیه تحقیق چیست؟
6- آیا داده ها پیوسته، رتبه ای و یا مقوله ای Categorical هستند؟
قبل از ادامه این مبحث لازم است مفهوم چند واژه آماری را یاد آور شوم که زیاد وقت گیر نیست.
1- جامعه آماری: به مجموعه کاملی از افراد یا اشیاء یا اجزاء که حداقل در یک صفت مورد علاقه مشترک باشند ،گفته می شود.
2- نمونه آماری: نمونه بخشی از یک جامعة آماری تحت بررسی است که با روشی که از پیش تعیین شده است انتخاب میشود، به قسمی که میتوان از این بخش، استنباطهایی دربارة کل جامعه بدست آورد.
3- پارامتر و آماره: پارامتر یک ویژگی جامعه است در حالی که آماره یک ویژگی نمونه است. برای مثال میانگین جامعه یک پارامتر است. حال اگر از جامعه نمونهگیری کنیم و میانگین نمونه را بدست آوریم، این میانگین یک آماره است.
4- برآورد و آزمون فرض: برآوردیابی و آزمون فرض دو روشی هستند که برای استنباط درمورد پارامترهای مجهول دو جمعیت به کار می روند.
5- متغیر: ویژگی یا خاصیت یک فرد، شئ و یا موقعیت است که شامل یک سری از مقادیر با دسته بندیهای متناسب است. قد، وزن، گروه خونی و جنس نمونه هایی از متغیر هستند. انواع متغیر می تواند کمی و کیفی باشد.
6- داده های کمی مانند قد، وزن یا سن درجه بندی می شوند و به همین دلیل قابل اندازه گیری می باشند. داده های کمی نیز خود به دو دسته دیگر تقسیم می شوند:
الف: داده های فاصله ای (Interval data)
ب: داده های نسبتی (Ratio data)
7- داده های فاصله ای: به عنوان مثال داده هایی که متغیر IQ (ضریب هوشی) را در پنج نفر توصیف می کنند عبارتند از: 80، 110، 75، 97 و 117، چون این داده ها عدد هستند پس داده های ما کمی اند اما می دانیم که IQ نمی تواند صفر باشد و صفر در اینجا فقط مبنایی است تا سایر مقادیر IQ در فاصله ای منظم از صفر و یکدیگر قرار گیرند پس این داده ها فاصله ای اند.
8- داده های نسبتی: داده های نسبتی داده هایی هستند که با عدد نوشته می شوند اما صفر آنها واقعی است. اکثریت داده های کمی این گونه اند و حقیقتاً دارای صفر هستند. به عنوان مثال داده هایی که متغیر طول پاره خط بر حسب سانتی متر را توصیف می کنند عبارتند از: 20، 15، 35، 8 و 23، چون این داده ها عدد هستند پس داده های ما کمی اند و چون صفر در اینجا واقعاً وجود دارد این داده نسبتی تلقی می شوند.
9- داده های کیفی مانند جنس، گروه خونی یا ملیت فقط دارای نوع هستند و قابل بیان با استفاده از واحد خاصی نیستند. داده های کیفی خود به دو دسته دیگر تقسیم می شوند:
الف: داده های اسمی (Nominal data)
ب: داده های رتبه ای (Ordinal data)
10- داده های رتبه ای Ordinal: مانند کیفیت درسی یک دانش آموز (ضعیف، متوسط و قوی) و یا رتبه بندی هتل ها ( یک ستاره، دو ستاره و ...)
11- داده های اسمی (nominal ) که مربوط به متغیر یا خواص کیفی مانند جنس یا گروه خونی است و بیانگر عضویت در یک گروها category خاص می باشد. (داده مقوله ای)
12- متغیر تصادفی گسسته و پیوسته: به عنوان مثال تعداد تصادفات جادهای در روز یک متغیر تصادفی گسسته است ولی انتخاب یک نقطه به تصادف روی دایرهای به مرکز مبدأ مختصات و شعاع 3 یک متغیر تصادفی پیوسته است.
13- گروه: یک متغیر می تواند به لحاظ بررسی یک ویژگی خاص در یک گروه و یا دو و یا بیشتر مورد بررسی قرار گیرد. نکته 1: دو گروه می تواند وابسته و یا مستقل باشد. دو گروه وابسته است اگر ویژگی یک مجموعه افراد قبل و بعد از وقوع یک عامل سنجیده شود. مثلا میزان رضایت شغلی کارکنان قبل و بعد از پرداخت پاداش و همچنین اگر در مطالعات تجربی افراد از نظر برخی ویژگی ها در یک گروه با گروه دیگر همسان شود.
14- جامعه نرمال: جامعه ای است که از توزیع نرمال تبعیت می کند.
15- توزیع نرمال: یکی از مهمترین توزیع ها در نظریه احتمال است. و کاربردهای بسیاری در علوم دارد.
فرمول این توزیع بر حسب دو پارامتر امید ریاضی و واریانس بیان می شود. منحنی رفتار این تابع تا حد زیادی شبیه به زنگ های کلیسا می باشد. این منحنی دارای خواص بسیار جالبی است برای مثال نسبت به محور عمودی متقارن می باشد، نیمی از مساحت زیر منحنی بالای مقدار متوسط و نیمه دیگر در پایین مقدار متوسط قرار دارد و اینکه هرچه از طرفین به مرکز مختصات نزدیک می شویم احتمال وقوع بیشتر می شود.
سطح زیر منحنی نرمال برای مقادیر متفاوت مقدار میانگین و واریانس فراگیری این رفتار آنقدر زیاد است که دانشمندان اغلب برای مدل کردن متغیرهای تصادفی که با رفتار آنها آشنایی ندارند، از این تابع استفاده می کنند. به عنوان مثال در یک امتحان درسی نمرات دانش آموزان اغلب اطراف میانگین بیشتر می باشد و هر چه به سمت نمرات بالا یا پایین پیش برویم تعداد افرادی که این نمرات را گرفته اند کمتر می شود. این رفتار را بسهولت می توان با یک توزیع نرمال مدل کرد.
اگر یک توزیع نرمال باشد مطابق قضیه چی بی شف 26.68 % مشاهدات در فاصله میانگین، مثبت و منفی یک انحراف معیار قرار دارد. و 44.95 % مشاهدات در فاصله میانگین، مثبت و منفی دو انحراف معیار قرار دارد. و 73.99 % مشاهدات در فاصله میانگین، مثبت و منفی سه انحراف معیار قرار دارد.
نکته 1: واضح است که داده های رتبه ای دارای توزیع نرمال نمی باشند.
نکته 2: وقتی داده ها کمی هستند و تعداد نمونه نیز کم است تشخیص نرمال بودن داده ها توسط آزمون کولموگروف – اسمیرنف مشکل خواهد شد.
16- آزمون پارامتریک: آزمون های پارامتریک، آزمون های هستند که توان آماری بالا و قدرت پرداختن به داده های جمع آوری شده در طرح های پیچیده را دارند. در این آزمون ها داده ها توزیع نرمال دارند. (مانند آزمون تی).
17- آزمون های غیرپارامتری: آزمون هائی می باشند که داده ها توزیع غیر نرمال داشته و در مقایسه با آزمون های پارامتری از توان تشخیصی کمتری برخوردارند. (مانند آزمون من – ویتنی و آزمون کروسکال و والیس)
نکته3: اگر جامعه نرمال باشد از آزمون های پارامتریک و چنانچه غیر نرمال باشد از آزمون های غیر پارامتری استفاده می نمائیم.
نکته 4: اگر نمونه بزرگ باشد، طبق قضیه حد مرکزی جتی اگر جامعه نرمال نباشد می توان از آزمون های پارامتریک استفاده نمود.








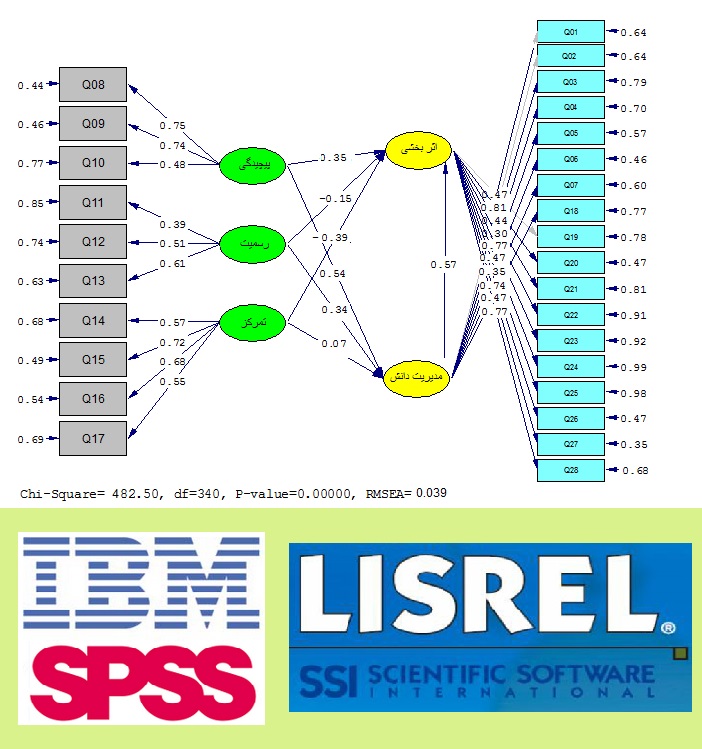
 نمونه تحلیل پرسشنامه با لیزرل
نمونه تحلیل پرسشنامه با لیزرل





