شاخص ماهالانوبیس در مدل سازی معادلات ساختاری
دو مشکلی اساسی هنگام استفاده از فاصله اقلیدسی وجود دارد. مشکل اول ناشی از وجود رابطه یا همبستگی بین محورها است. اگر مقدارهای مربوط به محور افقی و عمودی با یکدیگر ارتباط یا همبستگی داشته باشند، فاصله اقلیدسی بزرگتر از حالتی است که مستقل باشند. به این ترتیب به نظر میرسد که فاصله اقلیدسی وزن بیشتری به مشاهدات مرتبط با هم میدهد. به این ترتیب اطلاع از مختصات یک نقطه میتواند در تعیین مختصات نقطه دیگر کمک کند و به این ترتیب آگاهی از مختصات یک نقطه میتواند برای جایگزین اطلاعات مربوط به نقطه دیگر باشد. در حالیکه در فاصله اقلیدسی درکی نسبت به این موضوع وجود ندارد و فاصلهها دوباره محاسبه شده و میتواند در مجموع، میانگین فاصلهها را تحت تاثیر قرار دهد. البته از آنجایی که متغیرها یا مولفههای مشخص شده در مولفههای اصلی مستقل از یکدیگر ایجاد میشوند، معمولا این مشکل در این حالت بروز نمیکند.
مشکل دوم و اساسی هنگام استفاده از فاصله اقلیدسی، محاسبه میانگین و انحراف استاندارد دادهها است. اگر واقعا مجموعه داده شامل نقاط پرت باشد، میانگین و انحراف استاندارد را تحت تاثیر خود قرار داده و محاسبات را دچار مشکل میکنند. توجه داشته باشید که دادههای پرت واقعا متعلق به توزیع اصلی دادهها نیستند. مقدارهای پرت ممکن است بر اثر خطای اندازهگیری یا موارد خاص بوجود آمده باشند که نمیتوانند گویای رفتار واقعی و دائمی پدیده تصادفی باشند. برای خروج از این بحران از فاصله ماهالانوبیس استفاده میکنیم. این تابع فاصله توسط چاندار ماهالانوبیس، دانشمند و آمار شناسی هندی در سال 1936 میلادی معرفی شد.

چاندار ماهالانوبیس- دانشمند و آمار شناس هندی
مدل یابی معادله ساختاری یک تکنیک تحلیل چند متغیری بسیار کلی و نیرومند از خانواده رگرسیون چند متغیری و به بیان دقیقتر بسط “مدل خطی عمومی” (General linear model) است که به پژوهشگر امکان میدهد مجموعه ای از معادلات رگرسیون را به گونه هم زمان مورد آزمون قرار دهد. مدل یابی معادله ساختاری،روشهای تحلیل عاملی، همبستگی کانونی و رگرسیون چندمتغیری را با یکدیگر ترکیب می کند.
یکی از قویترین و مناسبترین روشهای تجزیه و تحلیل در تحقیقات علوم رفتاری و اجتماعی، تجزیه و تحلیل چند متغیره است. زیرا ماهیت این گونه موضوعات چند متغیره بوده و نمیتوان آنها را با شیوه دو متغیری (که هر بار یک متغیر مستقل با یک متغیر وابسته در نظر گرفته میشود) حل نمود. تجزیه و تحلیل چند متغیره به یک سری روشهای تجزیه و تحلیل اطلاق میشود که ویژگی اصلی آنها تجزیه و تحلیل همزمان k متغیر مستقل و n متغیر وابسته است. مدل یابی معادله ساختاری یک رویکرد جامع برای آزمون فرضیههایی درباره روابط متغیرهای آشکار (مشاهده شده) و پنهان (نهفته یا مکنون) است که گاه تحلیل ساختاری کوواریانس، مدل یابی علّی و گاه نیز لیزرل (LISREL) نامیده شده است؛ اما اصطلاح غالب در این روزها، مدلیابی معادله ساختاری یا به گونه خلاصه SEM است.
از طریق این روش میتوان قابل قبول بودن مدلهای نظری را در جامعههای خاص با استفاده از دادههای همبستگی، غیر آزمایشی و آزمایشی آزمود. این روش برآوردهایی از پارامترهای مدل (ضرایب مسیر و عبارات خطا) و همچنین چند شاخص برای نیکویی برازش فراهم میکند و با بهرهگیری از دادههای تجربی امکان آزمون مدلهای تدوین شده را به عنوان یک کل فراهم آورده و با شاخصهایی که در اختیار پژوهشگر قرار میدهد، وی را در اصلاح و بهبود مدل راهنمایی میکند.
انواع مدل در مدل یابی معادله ساختاری
مدل یابی معادله ساختاری را می توان برای آزمون انواع مختلفی از مدلها مانند مدلهای رگرسیون، تحلیل مسیر، مدلهای تحلیل عاملی تاییدی، مدلهای عاملی مرتبه دوم، مدلهای MIMIC (مدلهای با شاخصهای چندگانه و علل چندگانه)، مدلهای چندسطحی، مدلهای گروههای چندگانه و …. به کار برد.
تحلیل مسیر
سول رایت (Sewall Wright) تحلیل مسیر را به عنوان روشی برای مطالعۀ تأثیرات مستقیم و غیرمستقیم متغیرهایی که علت گرفته شدهاند در متغیرهایی که معلول فرض شدهاند ساخت و پرداخت. باید در نظر داشت که از تحلیل مسیر برای کشف علتها استفاده نمیشود بلکه این روش در مورد مدلهایی به کار میرود که بر مبنای دانش و ملاحظات نظری تدوین شده باشند. تحلیل مسیر ابزار تحلیلی مهمی برای آزمودن نظریه هاست که از کاربرد آن محقق می تواند توافق الگویی از همبستگی ها را که از مجموعه ای از مشاهدات حاصل شده است، با یک مدل معین معلوم کند.
مدل مسیر: مدل مسیر دیاگرامی است که متغیرهای مستقل، میانجی یا واسطهای و وابسته را به هم مرتبط میکند. پیکانهای یکطرفه نشان دهندۀ علّیت بین متغیرهای برونزا یا واسطهای و متغیرهای وابسته هستند. پیکانها عبارتهای خطا را هم به متغیرهای درونزا مخصوص خود مرتبط میکنند. پیکانهای دو طرفه نشان دهنده همبستگی بین جفتهای متغیرهای برونزا هستند.
ضرایب مسیر: ضریب مسیر یک ضریب رگرسیون استاندارد (بتا) است که اثر مستقیم یک متغیر مستقل روی یک متغیر وابسته را در مدل مسیر نشان میدهد. بنابراین زمانی که مدل دو یا چند متغیر علّی دارد، ضرایب مسیر ضرایب رگرسیون پارهای هستند که میزان تأثیر یک متغیر روی متغیر دیگر را با کنترل سایر متغیرها در مدل اندازه میگیرد. برآوردهای مسیر میتوانند توسط رگرسیون حداقل مجذورات یا بیشینه درست نمایی برآورد شوند.
اثرات مستقیم و غیرمستقیم: ضرایب مسیر میتوانند برای تجزیه همبستگی بین دو متغیر به اثرات مستقیم و غیرمستقیم استفاده شوند. اثرهای غیرمستقیم مستلزم متغیرهای میانجی است.
رویکردهای مدل یابی معادله ساختاری (LISREL یا PLS)
به طور کلی در مدل یابی معادله ساختاری (SEM) برای برآورد پارامترهای مدل دارای دو نوع میباشد که عبارتند از: رویکرد مبتنی بر کوواریانس و رویکرد مبتنی بر واریانس.
رویکرد کوواریانس محور
روش کوواریانس محور که به عنوان نسل اول مدل یابی معادلات ساختاری شناخته شده است، به شدت به حجم نمونه بالا بستگی دارد و هر چه دادهها نرمالتر باشند، برازش بهتری را نشان میدهد. روش کوواریانس محور تلاش میکند تا اختلاف بین کوواریانسهای نمونه و آنچه که مدل نظری پیشبینی کرده است را به حداقل برساند. نرم افزار LISREL یکی از ﻗﻮیترین و ﻣﻨﺎﺳﺐﺗﺮین رویکردهای کوواریانس محور برای تجزیه و تحلیل در ﺗﺠﺰیه و تحلیل ﭼﻨﺪ متغیره اﺳﺖ. زیرا ﻣﺎهیت این ﮔﻮﻧﻪ ﻣﻮﺿﻮﻋﺎت، دارای چند متغیر بوده و این متغیرها نیز با هم ارتباطات پیچیدهتری دارند و ﻧﻤﯽﺗﻮان آﻧﻬﺎ را ﺑﺎ شیوهای که ﺗﻨﻬﺎ ارتباط میان یک متغیر ﻣﺴﺘﻘﻞ ﺑﺎ یک متغیر واﺑﺴﺘﻪ بررسی میشود، ﺣﻞﻧﻤﻮد. روش کوواریانس محور برای توسعه نظریه مناسبتر است و با MPLUS ، AMOS وEQS نیز قابل اجرا میباشد.
مفاهیم مدل یابی معادله ساختاری کوواریانس محور
متغیر آشکار (مشاهده شده)
متغیرهایی که با مشاهده مستقیم رویداد بدست میآیند که به عنوان شاخص اندازهگیری یک متغیر پنهان ایفای نقش میکنند و در دیاگرام مسیر با مستطیل مشخص میشوند.

متغیرهایی که مستقیماً قابل مشاهده نیستند. متغیرهای پنهان از طریق پیوند با متغیرهای قابل اندازهگیری (آشکار) بررسی و در دیاگرام مسیر با دایره یا بیضی مشخص میشوند. متغیرهای پنهان در مدل معادلات ساختاری به دو دسته بیرونی و درونی تقسیم میشوند.

متغیرهای پنهان بیرونی: متغیرهایی هستند که علت تغییرات آنها در مدل منظور نشده و تحت تأثیر متغیرهای دیگر مدل قرار ندارند.
متغیرهای پنهان درونی: متغیرهایی که تحت تأثیر یک یا چند متغیر دیگر قرار دارند.
خطای باقیمانده
خطاهای باقیمانده نشاندهنده خطای تصادفی متغیرهای آشکار و نیز متغیرهای پنهان هستند که درون خطوط بسته قرار نمیگیرند.
خطوط کشیده شده به سمت متغیرهای آشکار بیانگر خطاهای اندازهگیری هستند.
خطوط کشیده شده به سمت متغیرهای پنهان بیانگر واریانسهای باقیمانده یا از دست رفته هستند.

توجه: در مدل یابی معادله ساختاری، از خطوط راست (فلشهای یکطرفه) برای نشان دادن روابط علی یا تأثیر یک متغیر بر متغیر دیگر استفاده میشود.

خطوط منحنی (فلشهای دوطرفه) برای نشان دادن همبستگیها استفاده میشود.
مدل اندازهگیری:
مدل اندازهگیری روابط بین متغیرهای پنهان و آشکار (مولفههای یک متغیر پنهان) را تعریف میکند. مدل اندازهگیری دارای دو نوع میباشد:
مدل اندازهگیری X : روابط بین متغیر پنهان مستقل و متغیرهای آشکار مربوط به آن را نشان میدهد.
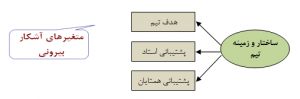
شکل ۱: مدل اندازهگیری X برای متغیر ساختار و زمینه تیم
مدل اندازهگیری Y : روابط بین متغیر پنهان وابسته و متغیرهای آشکار مربوط به آن را نشان میدهد.شکل ۱: مدل اندازهگیری X برای متغیر ساختار و زمینه تیم

شکل ۲: مدل اندازهگیری Y برای متغیر فراشناخت تیمی
مدل ساختاری (تحلیل مسیر):
مدل ساختاری، روابط بین متغیرهای پنهان را مشخص میکند.
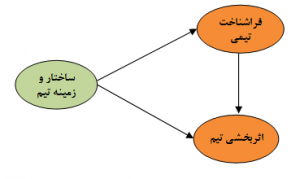 شکل ۳: مدل ساختاری
شکل ۳: مدل ساختاری
مدل عمومی معادله ساختاری
این مدل ترکیب دو مدل اندازهگیری و ساختاری است و در آن هم روابط بین متغیرهای پنهان با متغیرهای آشکار (مدل اندازهگیری) و هم روابط بین متغیرهای پنهان (مدل ساختاری) مورد توجه قرار میگیرد.
نمونهای از یک مدل عمومی معادله ساختاری
پژوهشی رابطه سه متغیر پنهان A، B وC به صورت زیر بررسی شده است:
- متغیر پنهان بیرونی A متغیر مستقل است که بر هر دو متغیر پنهان درونی B و C تاثیر میگذارد.
- برای اندازهگیری متغیر A از سه متغیر آشکار (شاخص) X1 ، X2 و X3 استفاده شده است.
- برای اندازهگیری متغیر B از سه متغیر آشکار (شاخص) Y1 ، Y2 و Y3 استفاده شده است.
- برای سنجش متغیر پنهان C از سه متغیر آشکار (شاخص) Y4 ، Y5 و Y6 استفاده شده است.
- ضریب مسیر بین دو متغیر پنهان وابسته با β و ضریب مسیر بین متغیر پنهان مستقل و وابسته با γ نشان داده میشود.
- ارتباط بین هر متغیر پنهان با متغیرهای آشکار مربوطه با حرف λ نشان داده که به آنها بار عاملی گفته میشود.
- ε نشان دهنده خطا (باقیمانده) برای متغیر آشکار درونی
- δ نشان دهنده خطا (باقیمانده) برای متغیر آشکار بیرونی
- ζ نشان دهنده واریانس خطا (باقیمانده) برای متغیر پنهان درونی
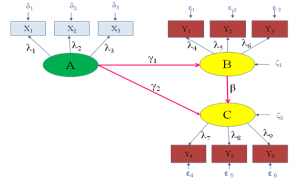
شکل ۴: نمونهای از یک مدل عمومی معادلات ساختاری براساس نمادها
مراحل مدل یابی معادله ساختاری کوواریانس محور
مرحله ۱: تدوین مدل
تدوین مدل براساس تئوری صورت میگیرد. در تدوین مدل، تعداد متغیرهای پنهان مدل، تعداد متغیرهای آشکار، روابط بین متغیرهای پنهان و آشکار مربوطه، الگوی روابط بین متغیرهای پنهان و محدودیتهای مدل (مشخصکردن پارامترهای ثابت، آزاد و مقید مناسب) مشخص میشود.
تعداد متغیرها در تدوین مدل
تعداد متغیرها به موضوع مورد مطالعه، هدف تحقیق و امکان سنجش این متغیرها بستگی دارد. در مجموع هرچه مدل طراحی شده پیچیدهتر باشد، دستیابی به برازش مدل مشکلتر میشود. ضمن اینکه باید به خاطر داشت که هرچه تعداد متغیر در یک مدل بیشتر باشد باید حجم نمونه نیز افزایش یابد. هرچند قاعده قطعی برای تعیین تعداد متغیرهای مدل وجود ندارد، اما عدهای معتقدند که در یک مدل نباید بیش از ۲۰ متغیر وارد کرد یعنی مثلاً ۵ یا ۶ متغیر به عنوان متغیرهای نهفته و هر متغیر ۳ تا ۴ شاخص را به خود اختصاص دهد.
مرحله ۲: تشخیص مدل (مشخصسازی)
تشخیص مدل یعنی آیا برای هریک از پارامترهای آزاد، میتوان یک مقدار منحصر به فرد از روی دادهها به دست آورد. براساس این تعریف سه نوع مدل خواهیم داشت:
مدلهای فرومشخص (under-identified): یک برآورد واحد برای هر پارامتر ناممکن باشد. یا به عبارتی اطلاعات مورد نیاز برای حل کردن پارامترها ناکافی باشد.
مدلهای کاملاً مشخص (just-identified): برای هر پارامتر واحد میتوان یک مقدار واحد برآورد کرد. یا به عبارتی تعداد معادلات با تعداد پارامترهای مورد تخمین برابر است.
مدلهای فرامشخص (over-identified): مدلهایی که برای هر پارامتر بیش از یک جواب دارند. یعنی تعداد پارامترهای مدل کمتر از مشاهدات است.
قاعده حسابی برای تشخیص مدل: تعداد پارامترهایی که باید برآورد شوند (پارامترهای آزاد) نباید از تعداد واریانسها و کوواریانسهای نمونه بیشتر باشد. اگر تعداد متغیرهای مشاهده شده (شاخصها) برابر P باشد، بنابراین از طریق فرمول زیر میتوان تعداد کل واریانسها و کوواریانسهای ممکن را برآورد نمود.
p × (p+1)〉 / ۲〉= تعداد کل واریانسها و کوواریانسهای نمونه
- مدل کاملا مشخص از نظر علمی مطلوب نیست. زیرا درجه آزادی (df) آن صفر میشود و هرگز نمیتواند رد شود. در عمل محققان باید مدلهای فرامشخص که دارای درجه آزادی مثبت هستند را تجزیه و تحلیل کنند. مدلهایی که مشخص نیستند باید دوباره تدوین شوند.
- برای اینکه مدلی مشخص باشد باید هر عامل حداقل ۳ شاخص داشته باشد.
- شرط لازم و کافی برای مشخص سازی وقتی فراهم میشود که هر متغیر مشاهده شده (شاخص) فقط و فقط یک متغیر پنهان (عامل) را اندازهگیری کند.
مرحله ۳: برآورد مدل
برآورد مدل شامل تکنیکهایی است که برای برآورد پارامترهای مدل استفاده میشوند. برآورد پارامترها آنقدر تکرار میشود تا مدل موردنظر در یک مجموعه نهایی از پارامترهای برآورد شده همگرا شود.
روشهای برآورد مدل
- (Maximum Likelihood (ML: متداولترین روش برآورد و مستقل از مقیاس دادهها است. اگر متغیرهای مشاهده شده نرمال و خطی باشند و بیش از ۱۰۰ مورد وجود داشته باشد، از این روش میتوان استفاده کرد.
- (Generalized Least Squares (GLS: نتایجی مشابه روش ML ارائه میکند و با حجم نمونههای کوچکتر قابل کاربرد است.
- (Unweighted Least Squares (ULS : زمانی مناسب است که تمام متغیرهای مشاهده شده با یک مقیاس واحد اندازهگیری شده باشند.
- (Weighted Least Squares (WLS و (Diagonal weighted Least Squares (DWLS: وابسته به پیش فرض نرمال بودن نیستند و به حجم نمونه بسیار بالا (بیش از ۱۰۰۰ مورد) نیاز دارند.
مرحله ۴: آزمون مدل
یک بخش مهم در فرایند برآورد، ارزیابی برازش مدل است. منظور از برازش مدل این است که تا چه حد یک مدل با دادههای نمونه سازگاری و توافق دارد. بدین منظور از شاخصهای برازش استفاده میشود.
در صورتی که برازش مدل قابل قبول باشد، تخمین پارامترها مورد بررسی قرار میگیرند. یعنی نتایج بخش اندازهگیری و ساختاری مدل ارزیابی میشوند. نسبت تخمین هر پارامتر به خطای استاندارد آن بوسیله آماره t نشان داده میشود. برای اینکه پارامتر موردنظر قابل قبول یا به عبارتی معنادار باشد، باید قدرمطلق مقدار t آن بزرگتر یا مساوی ۱٫۹۶ باشد. بنابراین شاخصها از دقت لازم برای اندازهگیری سازههای نهفته تحقیق برخوردارند.
آزمونهای برازندگی مدل کلی
گرچه انواع گوناگونی از آزمونها که به آنها شاخصهای برازش گفته میشود، در حال توسعه و تکامل میباشند اما هنوز درباره حتی یک آزمون بهینه نیز توافق همگانی وجود ندارد. تصمیمگیری درباره برازش یک مدل براساس چند شاخص و نه یک شاخص انجام میگیرد. بنابراین برای ارزیابی برازش مدل، ضروری است تعداد متنوعی از شاخصها گزارش شود. زیرا شاخص های مختلف، جنبههای متفاوتی از برازش مدل را انعکاس میدهند. برخی از این شاخصها عبارتند از:
جدول۱: انواع شاخصهای برازش مدل و مقدار مجاز آنها
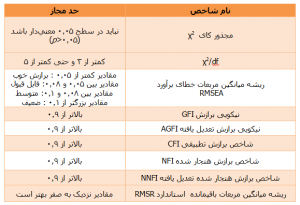
شاخصهای دیگری نیز در خروجی نرم افزار لیزرل دیده میشوند که برخی مثلAIC ،CAIC و ECVI برای تعیین برازندهترین مدل از میان چند مدل مورد توجه قرار میگیرند برای مثال مدلی که دارای کوچکترینAIC ،CAIC و ECVI باشد برازندهتر است. مقدار آماره ECVI به خودی خود قابل قضاوت نیست و برای نتیجهگیری درباره برازش مدل با مقادیر بدست آمده برای مدل استقلال و مدل اشباع شده مقایسه میگردد. مدلی که دارای کوچکترین CAIC و AIC باشد (هرچه به صفر نزدیکتر باشند)، برازندهتر است. برخی از شاخصها نیز به شدت وابسته به حجم نمونهاند و در حجم نمونههای بالا میتوانند معنا داشته باشند.
مرحله ۵: اصلاح مدل
گام نهایی اصلاح مدل نامیده میشود. در صورتی که مدل از برازش ضعیفی برخوردار باشد، با استفاده از اطلاعات حاصل از خروجی برنامه، جهت بهبود مدل تغییراتی در آن اعمال میشود.
منابع:
- کلانتری، خلیل (۱۳۸۸). مدل یابی معادله ساختاری در تحقیقات اجتماعی-اقتصادی. تهران: انتشارات فرهنگ صبا. چاپ اول.
- هومن، حیدرعلی (۱۳۸۸). مدل یابی معادله ساختاری با کاربرد نرمافزار لیزرل. تهران: انتشارات سمت. چاپ سوم.
- شوماخر، راندال ای و لومکس، ریچارد جی (۱۳۸۸). مقدمهای بر مدلسازی معادله ساختاری. مترجم: وحید قاسمی. تهران: انتشارات جامعه شناسان. چاپ اول. سال انتشار به زبان اصلی، ۲۰۰۴٫
- میرز، گامست، و گارینو (۲۰۰۶). پژوهش چندمتغیری کاربردی طرح و تفسیر. ترجمه شریفی و همکاران ۱۳۹۱. انتشارات رشد.
- کرلینجر، پدهازر (۱۹۸۲). رگرسیون چندمتعیری در پژوهش رفتاری. ترجمه حسن سرایی ۱۳۸۶. انتشارات سمت.
- Bollen, K. A. (1989). Structural equations with latent variables. New York: Wiley.
رویکرد واریانس محور یا حداقل مربعات جزئی (PLS)
PLS یا روش حداقل مربعات جزئی (Partial Least Square) یک رویکرد واریانس محور برای مدل یابی معادله ساختاری است، این تکنیک امکان بررسی روابط متغیرهای پنهان و شاخصها (متغیرهای قابل مشاهده) را بصورت همزمان فراهم می سازد. این روش را میتوان در شرایطی که حجم نمونه کم بوده و متغیرها حالت نرمال ندارند (البته در مدلهای ترکیبی یا Formative شرط نرمال بودن حائز اهمیت نمیباشد)، به کار برد. PLS شاخصهای برازش مدل را در اختیار محقق قرار نمیدهد، بنابراین برای پیشبینی مناسبتر است.
شاخصهای برازش این رویکرد مربوط به بررسی کفایت مدل در پیشبینی متغیرهای وابسته میشوند؛ مانند شاخصهای اشتراک (Communality) و افزونگی (Redundancy) یا شاخصGOF می باشد. در واقع این شاخصها نشان می دهند که برای مدل اندازه گیری شاخصها تا چه حد توانائی پیشبینی سازه زیربنایی خود را دارند و برای مدل ساختاری، متغیرهای بیرونی تا چه حد و با چه کیفیتی توانائی پیشبینی متغیرهای درنی مدل را دارند. رویکرد واریانس محور با نرمافزارهایی مانند پی ال اس گراف (PLS Graphing)، اسمارت پی ال اس (Smart- PLS)، رپ پی ال اس (Warp PLS) و ویژوال پی ال اس (Visual PLS) قابل اجرا میباشد.
حجم نمونه در روش حداقل مربعات جزئی PLS
در مدلیابی معادله ساختاری به روش حداقل مربعات جزئی برخلاف روش قبلی به حجم نمونه بالایی نیاز نداریم.
چین و نیوزتد (۱۹۹۹) در یک مطالعه شبیهسازی مونت کارلو بر روی PLS با نمونههای کوچک نشان دادند که این رویکرد میتواند برای حجم نمونه ۲۰ تایی نیز اطلاعاتی درباره تناسب شاخصها فراهم آورد. با این حال با در نظر گرفتن مشکل پایداری در مقیاس بزرگ، هنوز این مدل با محدودیت هایی روبروست. با وجود اینکه PLS برای نمونههای خیلی کوچک و یا موقعی که موارد نسبت به متغیرهای مشاهده شده کمتر باشد قابل استفاده است، اما تکیه بر نمونههای کوچک میتواند نتایج ضعیفی فراهم کند. نمونههای بزرگتر، برآوردهای PLS را قابل اطمینانتر میسازد. میانگین میزان خطای مطلق در PLS با افزایش حجم نمونه کاهش می یابد. حجم نمونه کوچک برای ضرایب مسیر کوچک کافی نیست، در چنین مواردی حجم نمونه برابر با روش کوواریانس محور مورد نیاز است.
محققان دو روش را برای تعیین حداقل نمونه لازم در PLS پیشنهاد میکنند:
- حجم نمونه بزرگتر یا مساوی ۱۰ برابر تعداد شاخصهای مدل اندازهگیریای که دارای بیشترین شاخص در میان مدلهای اندازهگیری مدل اصلی پژوهش است.
- حجم نمونه بزرگتر یا مساوی ۱۰ برابر بیشترین تعداد مسیرهای ساختاری که به یک متغیر (سازه) در مدل مسیر درونی ختم میشوند.
مدلهای اندازهگیری انعکاسی (Reflective) و مدلهای ترکیبی (Formative)
یکی از مهمترین تفاوتهای عمده بین مدلهای کوواریانس محور و PLS در شاخصهای انعکاسی (Reflective) و ترکیبی (Formative) میباشد. در روشهای کوواریانس محور، مدل ترکیبی وجود ندارد.
- مدل اندازهگیری انعکاسی ریشه در نظریه آزمون کلاسیک و روانسنجی دارد. این مدل شامل متغیرهای پنهانی است که نشانگر صفات، شخصیت یا نگرشها هستند و نمود آن ها توسط متغیرهای دیگر نشان داده میشوند. در این نوع مدل ها جهت پیکان از متغیر پنهان (سازه) به سمت متغیرهای مشاهده شده است؛ یعنی فرض بر این است که اندازهگیریهای مشاهده شده، تغییر در متغیر پنهان را منعکس میکنند. به عبارت دیگر تغییر در متغیر پنهان سبب تغییر در متغیرهای مشاهده شده میشود. در مدلهای انعکاسی باید همبستگی مثبت و نسبتا بالایی بین متغیرهای مشاهده شده وجود داشته باشد.
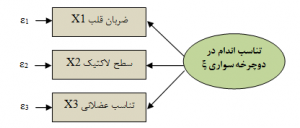
شکل ۵: نمونهای از یک مدل اندازهگیری انعکاسی
- مدلهای اندازهگیری ترکیبی شامل متغیرهای مشاهده شدهای هستند که علت یا ایجاد کننده متغیرهای پنهان میباشند. یعنی متغیرهای تشکیلدهنده به عنوان متغیرهای علی در نظر گرفته شدهاند که بر شکلگیری متغیر پنهان تاثیر دارند. در مقابل مدلهای انعکاسی، در مدلهای ترکیبی بین متغیرهای مشاهده شده، همبستگی میتواند مثبت، منفی یا صفر باشد. به عنوان مثال متغیر پنهان استرس زندگی را درنظر بگیرید. این متغیر میتواند از ترکیب متغیرهای مشاهده شدهای مانند از دست دادن شغل، طلاق یا حوادث ناگوار در زندگی تشکیل شود. یعنی این عوامل بر استرس زندگی تاثیر میگذارند. اما نمره سازه مورد نظر از نمره سئوالات آن به دست میآید. جهت پیکان از متغیرهای مشاهده شده به سمت متغیر پنهان (سازه) است؛ یعنی تغییر در متغیرهای مشاهده شده سبب تغییر در متغیر پنهان میشود.
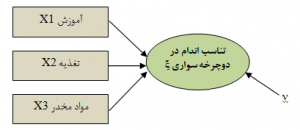
شکل ۶: نمونهای از یک مدل اندازهگیری ترکیبی
مدل درونی (Inner Model) و مدل بیرونی (Outer Model)
در مدل های PLS دو مدل آزمون می شود: مدلهای بیرونی و مدل های درونی. بخش اندازهگیری مدل که نمایشگر روابط بین متغیرهای پنهان با شاخصهایشان به دو صورت ترکیبی و انعکاسی میباشد، مدل بیرونی و بخش ساختاری مدل که نمایانگر رابطه بین متغیرهای مکنون است، مدل درونی نام دارد.
ارزیابی مدلها با استفاده از PLS
بررسی برازش مدلهای واریانس محور یا همان PLS در سه مرحله صورت میگیرد:
- ارزیابی مدل اندازه گیری (مدل بیرونی) انعکاسی یا ترکیبی: تعیین پایایی و روایی
- ارزیابی مدل ساختاری (مدل درونی)
- آزمون مدل کلی PLS
ارزیابی مدل اندازه گیری (مدل بیرونی)
در این مرحله، روای و پایایی مدل برحسب نوع مدل یعنی انعکاسی یا ترکیبی بودن آن تعیین میشود. معیارهای ارزیابی مدل اندازهگیری در جدول زیر ارائه شده است.
جدول ۲: معیارهای ارزیابی مدل اندازه گیری (مدل بیرونی)
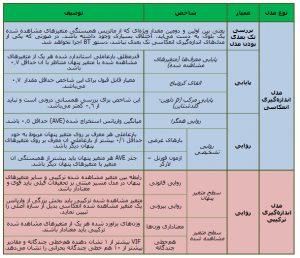
ارزیابی مدل ساختاری (مدل درونی)
در یک مدل مسیر فقط یک مدل ساختاری وجود دارد. پس از ارزیابی برآوردهای روایی و پایایی مدلهای اندازهگیری نوبت به ارزیابی مدل ساختاری میرسد. معیارهای آزمون مدل ساختاری در جدول زیر ارائه شدهاند:
جدول ۳: معیارهای ارزیابی مدل ساختاری (مدل درونی)
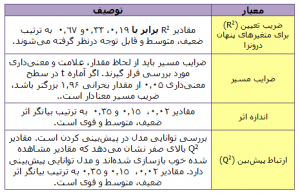
آزمون مدل کلی PLS
در PLS برخلاف روش کوواریانس محور شاخصی برای سنجش کل مدل وجود ندارد. البته تننهاوس و همکاران (۲۰۰۵) یک شاخص کلی به نام نیکویی برازش (GOF) را برای بررسی برازش مدل معرفی کردهاند. این شاخص را می توان با محاسبه متوسط R2 و متوسط مقادیر اشتراکی (Communality) از طریق فرمول زیر بدست آورد:
البته باید توجه داشت که این شاخص توانایی پیشبینی کلی مدل را مورد بررسی قرار میدهد. یعنی اینکه آیا مدل آزمون شده در پیشبینی متغیرهای پنهان درون زا موفق بوده است یا نه. وتزلس و همکاران (۲۰۰۹) مقادیر ۰٫۰۱، ۰٫۲۵ و ۰٫۳۶ را به ترتیب به عنوان مقادیر ضعیف، متوسط و قوی برای GOF معرفی نمودهاند.
منابع:
- محسنین، شهریار و اسفیدانی، محمد رحیم. (۱۳۹۳). معادلات ساختاری مبتنی بر رویکرد حداقل مربعات جزیی – به کمک نرم افزار Smart-PLS. تهران: مهربان نشر. چاپ اول.
- Henseler, Jörg; Ringle, Christian M; Sinkovics, Rudolf R. (2009). The use of partial least squares path modeling in international marketing, in Rudolf R. Sinkovics, Pervez N. Ghauri (ed.) New Challenges to International Marketing (Advances in International Marketing, Volume 20) Emerald Group Publishing Limited, pp.277 – ۳۱۹
- Nunnally, J. C., & Bernstein, I. H. (1994). Psychometric theory (3rd ed.). New York, NY: McGraw-Hill.

