نکات بسیار مهم آزمون های تعقیبی post hoc

POST_HOC

آزمون ANOVA یا تحلیل واریانس یک طرفه برای آزمون مقایسه میانگین یک متغیر کمی در بین بیش از دو گروه مستقل استفاده می شود. در حقیقت این آزمون تعمیم یافته همان آزمون T دو نمونه مستقل است و دارای همان پیش فرض ها می باشد و تنها تفاوت این است که میانگین متغیر های کمی در بیش از دو گروه مستقل با هم مقایسه می شوند. در مقاله آزمون F تحلیل واریانس یک طرفه یا ANOVA این آزمون به زبانی ساده و به صورت تفصیلی به همراه تفاسیر آن و در قالب یک فصل چهار کامل آموزش داده شد. اما نکته بسیار مهم بعد از خواندن آن مقاله این است که در آن مقاله بیان شد که آزمون تحلیل واریانس ANOVA  تنها به این سوال پاسخ می دهد که آیا بین گروه های مختلف مستقل تفاوت میانگین(متغیر کمی) وجود دارد یا ندارد؟ یعنی از کیفیت تفاوت میانگین اطلاعاتی به ما نمی دهد. (کیفیت تفاوت یعنی اینکه بیان کند بین کدام گروه ها تفاوت وجود دارد و جهت این تفاوت به کدام سمت است)

بنابراین برای رفع این مشکل باید از آزمون های تعقیبی مناسب استفاده نماییم. این آزمون های مکمل را Post hoc می خوانند اما زمانی که از درون نرم افزار می خواهیم دست به انتخاب آزمون های تعقیبی post hoc بزنیم با دو مشکل و ابهام مواجه هستیم.

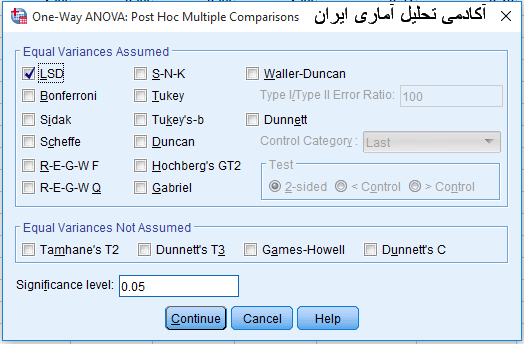شکل1) آژمون های تعقیبی post hoc

مشکل اول این است که دو دسته آزمون تعقیبی وجود دارد. 14 آزمون قسمت اول شکل 1 که با شرط برابری واریانس های گروه های مستقل متغیر کیفی می باشد و 4 آزمون قسمت دوم شکل 1 که با شرط عدم برابری واریانس های گروه های مستقل متغیر کیفی قرار داده شده است. همانطور که در مقالهآزمون F تحلیل واریانس یک طرفه یا ANOVAآموزش داده شد آزمون لوین این مشکل را حل می کند یعنی با شرط آماری زیر دست به انتخاب از یکی از دو دسته شکل 1 می زنیم.

واریانس های دو گروه با هم برابر هستند H₀:

واریانس های دو گروه با هم برابر نیستند H₁:

اما این مقاله به مشکل دوم می پردازد که متاسفانه حتی کتاب های روش تحقیق، نرم افزار، پایان نامه ها و مقالات هم این مشکل به صورت گسترده وجود دارد. این بخش از مقاله به بررسی این 18 آزمون تعقیبی به صورت تفصیلی و به زبان ساده می پردازد. منبع این مطلب کتاب روش پژوهش آقای دکتر محسن مرادی و خانم دکتر میر الماسی است که انشالله بزودی از طریق سایت در اختیار عزیزان قرار می گیرد. این کتاب به صورت ساده و جامع تلاش کرده گامی در جهت ارتقای روش پژوهش در ایران به سمت جلو بردارد.

لطفا محققین و خصوصا دانش پژوهان آکادمی تحلیل آماری ایران این توضیحات را با دقت مطالعه نمایند تا نکات بسیار مهم آزمون های تعقیبی post hoc که همان نحوه انتخاب ما از بین این آزمون ها می باشد را بیاموزند

آزمون های تعقیبی یا post hoc با فرض برابری واریانس های بین گروه ها

همانطور که در شکل بالا دیده می شود بعد از آزمون لوین اگر شرط H₀ تایید گردید به معنای این است که پراکندگی یا واریانس بین گروه ها با هم برابر است و محقق باید از 14 آزمون بالا با شرط برابری واریانس های بین گروه ها دست به انتخاب بزند. اما متاسفانه یک ایراد ساختاری وجود دارد که محققین به غلط عادت کرده اند که آزمونی مثل توکی را انتخاب و بدون توجه به علت و دلیل این انتخاب کار را تحلیل نمایند که این خود یک ایراد روش شناسی در بخش تجزیه و تحلیل داده ها است. اما سوال این است که کدام آزمون از این 14 آزمون را باید انتخاب نمود؟ برای پاسخ به این سوال باید با این 14 آزمون تعقیبی یا post hoc باید آشنا گردید.

1. آزمون :LSD

یا حداقل تفاوت معناداری فیشر: این آزمون بنا به نظر فیلد 2000 یکی از قدیمی ترین و قویترین آزمون های تعقیبی در بین 14 آزمون مربوطه است. او بیان می کند وقتی که متغیر کیفی یا factor که می خواهیم متغیر کمی خود را در بین گروه های آن مقایسه نماییم 3 وجهی باشد(مانند متغیر محل اسکان که در کلاس SPSS آکادمی تحلیل آماری به عنوان مثال مطرح شد)  این آزمون مناسب ترین آزمون است و با دقت و توان بالا تفاوت میانگین بین این سه گروه و نیز جهت تفاوت را از طریق علامت های حد بالا و پایین خود تشخیص می دهد. نکته اینجاست که اگر تعداد وجه های متغیر کیفی یا همان تعداد گروه های مستقلی که در آن تفاوت سنجی انجام می شود ، بیش از 3 تا باشد، بهتر است که از آزمون های دیگر استفاده گردد.(مرادی و میر الماسی، 1398، ص 602)

2. آزمون بونفرونی یا  Bonferroni

این آزمون نیز برای مقایسه میانگین گروه ها مستقل زیر 4 گروه مناسب است و درست مثل آزمون قبل از آماره t دو نمونه مستقل بین جفت های بین گروه ها استفاده می کند. فراموش نشود که کنتون (2019) معتقد است که آزمون بونفرونی تلاش می کند که با ایجاد تنظیم در طول آزمون مقایسه ای جفت جفت، از نمایش داده هایی که آز نظر آماری نادرست است خودداری نماید.(کنتون، 2019). مطابق با دسته بندی که در بخش قبل نمودیم این آزمون توان اندکی در قابلیت تشخیص تفاوت و تمایز بین گروه ها دارا است. یعنی تفاوت باید بسیار آشکار و چشمگیر باشد تا بتوان توسط این آزمون معناداری تفاوت بین گروه های مستقل را تاییدی نمود. این دلیلی محکم بر محافظه کار بودن این آزمون است. البته به دلیل انعطاف بالا و سادگی محاسبات در دسته آزمون های تعقیبی متداول قرار می گیرد. .(مرادی و میر الماسی، 1398، ص 602)

3. سیداک یا Sidak :

این آزمون نیز بر اساس آزمون t دو نمونه مستقل عمل کرده و تفاوت بین گروه های مستقل را به عنوان یک آزمون تعقیبی در بین گروه های مستقل تعیین وضعیت می کند. اما فیلد در سال 2000 در مطالعات خود بیان می کند که این آزمون در حقیقت تعدیل و اصلاح شده ی آزمون بونفرونی است و در حقیقت آزمونی میانه رو می باشد که نسبت به آزمون بونفرونی نیاز به تفاوت و تمایز کمتری بین گروه های مستقل دارد تا معناداری این تمایز را اعلام نماید، اما در دیگر ابعاد تفاوتی با آزمون بونفرونی ندارد.(کوناگین و باربین، 2006). برای مطالعه بیشتر جهت مقایسه دو آژمون بونفرونی و سیداک محققین عزیز آکادمی می توانند مقاله   Bonferroni’s and Sidak’s modified test را که توسط کوناگین و باربین از برزیل منتشر شده است را مطالعه نمایید.

4. شفه یا scheffe

دانش پژوهان و محققین عزیز همانطور که در کلاس های آکادمی تحلیل آماری بیان شد باید قبل از اجرا آزمون آنووا ANOVA و آزمون های تعقیبی آن ابتدا یک فراوانی ساده را با SPSS از متغیر کیفی و یا FACTOR خود بگیرند تا مشخص شود که آیا تعداد مشاهدات یا داده های گروه های مستقل با هم برابر است یا خیر. زیرا در بسیاری از اوقات حجم نمونه بین گروه های مستقلی که می خواهیم متغیر کمی خود را در بین آن ها فراوانی شماری نماییم، حجم نمونه هاینابرابری دارند. در این هنگام این آزمون شفه که مناسب‌ترین و دقیقترین نتایج را در اختیار محقق قرار می دهد. (مرادی و میر الماسی، 1398، ص 603) اشکال عمده این روش، محتاطانه یا محافظه‌کارانه بودن آن است. بدین معنی که چون آزمون شفه تمامی ترکیب‌های خطی احتمالی میانگین گروه‌ها را آزمون می‌کند، بنابراین، در این آزمون، صرفاً ترکیب‌های جفتی آزمون نمی‌شوند. در نتیجه آزمون شفه نسبت به سایر آزمون‌ها محافظه‌کارتر است. به همین خاطر، برای این که تفاوت بین میانگین‌ها معنی‌دار باشد، نیازمند میزان بالایی از این تفاوت هستیم. آزمون شفه را معمولا با آزمون توکی که در بخش های بعد با آن موجه خواهیم شد، مقایسه می کنند.همچنین، آزمون شفه، در مقایسه با آزمون توکی، در یک مثال کاملا یکسان و با داده های یکسان، فرض صفر را کمتر رد می‌کند.(شریفی و نجفی زند، 1390، 238)

در جمع بندی باید گفت که که این آزمون نسبت به آزمون توکی قابلیت کاربرد برای مقایسه گروه های مستقل با حجم نمونه های متفاوت و نابرابر را دارد. همچنین در این آژمون توزیع داده های می تواند نرمال و یا غیر نرمال باشد و حتی این آزمون نسبت به شرط برابری واریانس های گروه های مستقل حساسیتی ندارد. (مرادی و میر الماسی، 1398، ص 603)

.

5. آزمون F رایان – اینوت – گبریل – ولچ یا R-E-G-W-F

در آزمون پیش شرط این است که تعداد حجم نمونه یا همان تعداد مشاهدات جمع آوری شده در گروه های مستقل از هم با هم متوازن و برابر باشند. استفانی در سال 2017 بیان می کند که در این طرح از آماره F استفاده می شود. یه صورتی که این طرح مرحله به مرحله انجام می شود. ابتدا میانگین تمام گروه های مستقل محاسبه شده و سپس آماره F برای تمایز سنجی بین بزرگترین و کوچکترین میانگین بین گروه ها بررسی می گردد. اگر این آماره معنادار باشد به مرحله بعد رفته و تمایز بین بزرگترین و کوچکترین میانگین بعدی بررسی می گردد و زمانی تحلیل متوقف می شود که تفاوت بین میانگین ها در یکی از این مراحل معنادار نباشد. . (مرادی و میر الماسی، 1398، ص 604)

6. آزمون Q رایان – اینوت – گبریل – ولچ یا R-E-G-W-Q

این آزمون نیز مزاحلی چون آزمون قبلی دارد و معمولاً حجم نمونه یا همان تعداد مشاهدات جمع آوری شده در گروه های مستقل از هم باید با هم متوازن و برابر باشند.البته استفانی 2017 اعتقاد دارد که این آزمون نسبت به   R-E-G-W-F  ازتوان بالایی در تمایز گروه‌ها از همدیگر دارد و کنترل شدیدی هم بر میزان خطای نوع اول دارد(استفانی، 2017)

7. نیومن-کلز استودنت شده یا S-N-K

استیل و همکارانش در سال 1997 در مقاله ای پیرامون اصول آماری در روش های بایو متریک بیان کردند که که این آزمون از آزمون توکی گرفته شده است با این تفاوت که لیبرال تر است. معنای آزمون لیبرال این است که برخلاف آزمون های محافظه کار، تفاوت های اندک بین گروه های مستقل را تشخیص می دهد. یعنی در تفوت های اندک بین گروه های مستقل sig برای آن ها معنادار می شود. (مرادی و میر الماسی، 1398، ص 604) در این آزمون ابتدا میانگین‌ها از بالاترین تا پایین‌ترین مقدار مرتب می‌شوند و سپس تفاوت بین هر جفت میانگین محاسبه می‌شود. در نهایت نیز، ارزش مقایسه‌ای که برای هر جفت از میانگین‌ها به طور جداگانه محاسبه می‌شود، با هم مقایسه می‌گردند.

8. توکی یا Tukey

آزمون توکی یا HSD آزمون معناداری حقیقی تفاوت بین میانگین ها، یک روش مقایسه ی میانگین چند مرحله ای است. در آن ابتدا میانگین متغیر کمی در تمام گروه های مستقل از هم محاسبه شده و سپس اولویت بندی و مرتب می شوند. سپس در قالب یک روش محافظه کار میانگین تمام جفت های ممکن با هم تمایز سنجی می شوند و این تفاوت سنجی بین تمام جفت های میانگین ها مشابه با آزمون t است. این آزمون زمانی که تعداد گروه ها زیاد است یکی از بهترین آزمون های post hoc می باشد.همچنین این پیش فرض را نباید از خاطر برد که تنها زمانی میتوان از این آزمون تعقیبی بهره برد که حجم نمونه گروه ها با هم برابر باشد. (لینتون و هاردر[13]، 2007) متاسفانه این نکته ایست که بسیاری از کسانی که کار آماری پژوهش را انجام می دهند از آن غفلت می کنند و میتوان از آن به عنوان یک اشکال ساختاری در تجزیه تحلیل واریانس یک طرفه در تحقیقات ایران نام برد(مرادی و میر الماسی، 1398، ص 605)

9. بی توکی[14] Tukey’s b

این آزمون نیز یک روش مقایسه ی میانگین چند مرحله ای است. در آن ابتدا میانگین متغیر کمی در تمام گروه های مستقل از هم محاسبه شده و سپس اولویت بندی و مرتب می شوند. سپس در قالب یک روش محافظه کار میانگین تمام جفت های ممکن با هم تمایز سنجی می شوند و این تفاوت سنجی بین تمام جفت های میانگین ها مشابه با آزمون t است. تفاوت آن نسبت به آزمون توکی این است که پیش فرض برابر بودن حجم نمونه گروه ها در آن وجود ندارد. (لینتون و هاردر[15]، 2007)

10. دانکن[16]یا Duncan

در این آزمون پیش فرض برابر بودن حجم نمونه گروه ها در آن وجود ندارد. در این آزمون را که چند دامنه دانکن نیز می خوانند، به دلیل توان بالای آن در تشخیص تمایز بین میانگین در گروه های مستقل رد رشته هایی چون پزشکی، زیست، شیمی و فیزیک و …… به کرات استفاده می کنند. هرچند هایر و همکارانش در سال 2006 پیرامون این کاربرد بدلیل عدم کنتل چندان بالای این آزمون بر خطاها مورد انتقاد قرار دادند. (مرادی و میر الماسی، 1398، ص 606)

11. آزمون جی تی دو هاچبرگز یا [17] Hochberg’s GT2

این آزمون نیز درست مانند آزمون توکی یک روش مقایسه ی میانگین چند مرحله ای است که در آن ابتدا میانگین متغیر کمی در تمام گروه های مستقل از هم محاسبه شده و سپس اولویت بندی و مرتب می شوند. سپس میانگین تمام جفت های ممکن با هم تمایز سنجی می شوند و این تفاوت سنجی بین تمام جفت های میانگین ها مشابه با آزمون t است. تفاوتی که این آزمون با آزمون توکی دارد، این است که از بزرگترین قدر مطلق بین میانگین متغیر کمی در گروه های مستقل استفاده می‌کند. بنابراین عملا آزمون توکی توان بالاتری نسبت به این آزمون دارد. اما این آزمون زمانی بجای توکی کاربرد دارد که حجم نمونه ی گروه های مستقل بسیار متفاوت و نابرابر باشد. استیون این اختلاف بین مشاهدات را بیش از 200 مشاهده بیان نموده است. (مرادی و میر الماسی، 1398، ص 606)

12. گابریل[18] یا Gabriel

این آزمون نیز از بزرگترین قدر مطلق بین میانگین متغیر کمی در گروه های مستقل استفاده می‌کند و زمانی که حجم نمونه گروه های مستقل با هم نابرابر باشند، عموماً قوی تر از آزمون جی تی دو هاچبرگز می‌باشد. البته نباید فراموش کرد که این نابرابری نمیتواند بسیار زیاد باشد زیرا بنا به نظر استیون از دقت آزمون کاسته می شود و در آن صورت جی تی دو هاچبرگز اولویت دارد. (مرادی و میر الماسی، 1398، ص 607)

13. والر-دانکن[19] یا Waller-Duncan

یکی از معدود آزمون هایی که بجای آمار کلاسیک از آمار بیزین و پیش فرض های آن استفاده می کند، آزمون والر دانکن است. این آزمون که به آزمون تی والر-دانکن نیز معروف است، زمانی که اندازه‌های نمونه ی گروه های مستقل از هم با هم برابر نباشند استفاده می شود و در آن میانگین هارمونیک متغیر کمی در هز یک از گروه های مستقل از هم محاسبه شده و سپس آزمون t  برای جفت جفت گروه ها اجرا می شود. (مرادی و میر الماسی، 1398، ص 608)

14. دانت[20] یا Dunnett

این آزمون که یک آزمون t جهت مقایسه چندگانه جفتی است، در این آزمون میانگین تک تک گروه ها محاسبه می شود. سپس میانگین گروه آخر را به عنوان گروه کنترل قرار می دهند و میانگین تک تک گروه ها را با آزمون t با گروه کنترل مورد مقایسه و تفاوت سنجی قرار می دهند. (مرادی و میر الماسی، 1398، ص 608)

 

آزمون های تعقیبی یا post hoc با فرض عدم برابری واریانس های بین گروه ها

همانطور که در شکل بالا دیده می شود بعد از آزمون لوین اگر شرط H₀ رد گردید به معنای این است که پراکندگی یا واریانس بین گروه ها با هم برابر نیست و محقق باید از 4 آزمون پایین با شرط عدم برابری واریانس های بین گروه ها دست به انتخاب بزند.

آزمون مقایسه چندگانه که فرض عدم برابری واریانس ها را می‌پذیرند، شامل 4 آزمون می‌باشند که در زیر مشاهده می شود

1. تی. دو تمهنه[21] Tamhane’s T2
2. تی. سه دانت[22] یا Dunntt’s T3
3. جیمز – هوئل[23] یا Games-Howell
4. سی دانت[24] یا Dunnett’s C

از بین چهار آزمون بالا بلا شک رایج ترین و قویترین آزمون ،. جیمز هوئل می باشد و محقق باید آن را انتخاب کند. این آزمون حساسیتی روی برابری حجم نمونه گروه های مستقل را نیز ندارد.

[1] Fisher Least Significant Difference

[2] Field

[3] Bonferroni

[4] Kenton

[5] Sidak

[6] Conagin and Barbin

[7] scheffe

[8] Ryan-Einot-Gabriel-Welsch

[9] Studentized Newman Keuls

[10] Steel & et al

[11] Tukey

[12] Honestly significant differece

[13] Linton and Harder

[14] Tukey’s b

[15] Linton and Harder

[16] Duncan

[17] Hochberg’s GT2

[18] Gabriel

[19] Waller-Duncan

[20]  Dunnett

[21] Tamhane’s T2

[22] Dunntt’s T3

[23] Games-Howell

[24] Dunnett’s C

 

منبع:

مرادی،محسن, & میرالماسی،آیدا. (1398). روش پژوهش عملگرا (پژوهش کمی و کیفی) (اول). تهران: آکادمی تحلیل آماری ایران(مدرسه پژوهش کمی و کیفی). Retrieved from www.analysisacademy.com