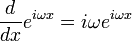نقاط سبز رنگ، نمونههایی از توزیع نرمال دومتغیرهاند و محور آبی رنگ، مختصات جدید در راستای قرار گرفتن بیشترین تغییرات نمونه بر روی مؤلفههای اصلی است.
تحلیل مولفههای اصلی (Principal Component Analysis – PCA) تبدیلی در فضای برداری است، که غالباً برای کاهش ابعاد مجموعهٔ دادهها مورد استفاده قرار میگیرد.
تحلیل مولفههای اصلی در سال ۱۹۰۱ توسط کارل پیرسون ارائه شد. این تحلیل شامل تجزیه مقدارهای ویژهٔ ماتریس کواریانس میباشد.
جزئیات
تحلیل مولفههای اصلی در تعریف ریاضی یک تبدیل خطی متعامد است که داده را به دستگاه مختصات جدید میبرد به طوری که بزرگترین واریانس داده بر روی اولین محور مختصات، دومین بزرگترین واریانس بر روی دومین محور مختصات قرار میگیرد و همین طور برای بقیه. تحلیل مولفههای اصلی میتواند برای کاهش ابعاد داده مورد استفاده قرار بگیرد، به این ترتیب مولفههایی از مجموعه داده را که بیشترین تاثیر در واریانس را دارند حفظ میکند. برای ماتریس داده  با میانگین تجربی صفر، که هر سطر یک مجموعه مشاهده و هر ستون دادههای مربوط به یک شاخصه است، تحلیل مولفههای اصلی به صورت زیر تعریف میشود:
با میانگین تجربی صفر، که هر سطر یک مجموعه مشاهده و هر ستون دادههای مربوط به یک شاخصه است، تحلیل مولفههای اصلی به صورت زیر تعریف میشود:
به طوری که  تجزیه مقدارهای منفرد ماتریس
تجزیه مقدارهای منفرد ماتریس  میباشد.
میباشد.
محدودیتهای تحلیل مولفههای اصلی
استفاده از تحلیل مولفههای اصلی منوط به فرضهایی است که در نظر گرفته میشود. از جمله:
ما فرض می کنیم مجموعه داده ترکیب خطی پایههایی خاص است.
- فرض بر این که میانگین و کواریانس از نظر احتمالاتی قابل اتکا هستند.
- فرض بر این که واریانس شاخصه اصلی داده است.
محاسبه مولفههای اصلی با استفاده از ماتریس کواریانس
بر اساس تعریف ارائه شده از تحلیل مولفههای اصلی، هدف از این تحلیل انتقال مجموعه داده X با ابعاد M به داده Y با ابعاد L است. بنابرین فرض بر این است که ماتریس X از بردارهای  تشکیل شده است که هر کدام به صورت ستونی در ماتریس قرار داده شده است. بنابرین با توجه به ابعاد بردارها (M) ماتریس دادهها به صورت
تشکیل شده است که هر کدام به صورت ستونی در ماتریس قرار داده شده است. بنابرین با توجه به ابعاد بردارها (M) ماتریس دادهها به صورت  است.
است.
محاسبه میانگین تجربی و نرمال سازی دادهها
نتیجه میانگین تجربی، برداری است که به صورت زیر به دست میآید:
که به طور مشخص میانگین تجربی روی سطرهای ماتریس اعمال شده است.
سپس ماتریس فاصله تا میانگین به صورت زیر به دست میآید:
که h برداری با اندازه 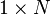 با مقدار ۱ در هرکدام از درایهها است.
با مقدار ۱ در هرکدام از درایهها است.
محاسبه ماتریس کواریانس
ماتریس کواریانس C با ابعاد  به صورت زیر به دست میآید:
به صورت زیر به دست میآید:
![C=\mathbb{E}[B\otimes B]=\mathbb{E}[B\cdot B^{\ast}]=\frac{1}{N}B\cdot B^{\ast}](http://upload.wikimedia.org/math/5/0/c/50c241be5d8692a9b08d288293bda0c5.png)
- به طوری که:
-
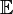 میانگین حسابی است.
میانگین حسابی است.
-
 ضرب خارجی است.
ضرب خارجی است.
-
 ماتریس ترانهاده مزدوج ماتریس
ماتریس ترانهاده مزدوج ماتریس  است.
است.
محاسبه مقادیر ویژه ماتریس کواریانس و بازچینی بردارهای ویژه
در این مرحله، مقادیر ویژه و بردارهای ویژه ماتریس کواریانس،  ، به دست میآید.
، به دست میآید.
V ماتریس بردارهای ویژه و D ماتریس قطری است که درایههای قطر آن مقادیر ویژه هستند. آنجنان که مشخص است، هر مقدار ویژه متناظر با یک بردار ویژه است. به این معنا که ماتریس V ماتریسی  است که ستونهای آن بردارهای ویژه میباشند و بردار ویژه
است که ستونهای آن بردارهای ویژه میباشند و بردار ویژه 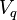 در ستون qام قرار دارد و مقدار ویژه qام یعنی درایهٔ
در ستون qام قرار دارد و مقدار ویژه qام یعنی درایهٔ  متناظر با آن است. بازچینی بردارهای ویژه بر اساس اندازهٔ مقادیر ویژه متناظر با آنها صورت میگیرد. یعنی بر اساس ترتیب کاهشی مقادیر ویژه، بردارهای ویژه بازچینی میشوند. یعنی
متناظر با آن است. بازچینی بردارهای ویژه بر اساس اندازهٔ مقادیر ویژه متناظر با آنها صورت میگیرد. یعنی بر اساس ترتیب کاهشی مقادیر ویژه، بردارهای ویژه بازچینی میشوند. یعنی 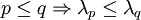
انتخاب زیرمجموعهای از بردارهای ویژه به عنوان پایه
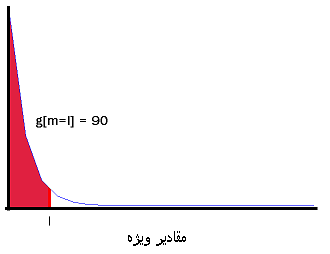 تحلیل مقادیر ویژه ماتریس کواریانس
تحلیل مقادیر ویژه ماتریس کواریانس
انتخاب زیرمجموعهای از بردارهای ویژه با تحلیل مقادیر ویژه صورت میگیرد. زیرمجموعه نهایی با توجه به بازچینی مرحله قبل به صورت  انتخاب میشود. در اینجا میتوان از انرژی تجمعی استفاده کرد که طبق آن
انتخاب میشود. در اینجا میتوان از انرژی تجمعی استفاده کرد که طبق آن
انتخاب l باید به صورتی باشد که حداقل مقدار ممکن را داشته باشد و در عین حال g مقدار قابل قبولی داشته باشد. به طور مثال میتوان حداقل l را انتخاب کرد که
بنابرین خواهیم داشت:
انتقال داده به فضای جدید
برای این کار ابتدا تبدیلات زیر را انجام می دهیم: ماتریس  انحراف معیار مجموعه داده است که میتواند به صورت زیر به دست بیاید:
انحراف معیار مجموعه داده است که میتواند به صورت زیر به دست بیاید:
سپس داده به صورت زیر تبدیل میشود:
-
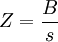 ‘
‘
که ماتریسهای  و
و  در بالا توضیح داده شده اند. دادهها میتوانند به ترتیب زیر به فضای جدید برده شوند:
در بالا توضیح داده شده اند. دادهها میتوانند به ترتیب زیر به فضای جدید برده شوند:
نرمافزارها
در نرمافزار متلب تابع princomp مولفههای اصلی را باز می گرداند.
تجزیه مقدارهای منفرد
به عنوان یک تجزیه و فاکتورگیری ماتریسی، تجزیۀ مقدارهای منفرد یا تجزیۀ مقدارهای تکین (Singular value decomposition) قدمی اساسی در بسیاری از محاسبات علمی و مهندسی بهحساب میآید.
مثالها
ماتریس زیر را در نظر میگیریم:
یکی از تجزیۀ مقدارهای منفرد این ماتریس به صورت زیر است:
یعنی داریم که

-
مقدار ویژه و بردار ویژه
مسأله مقادیر ویژه (Eigenvalue problem) (یا مسأله مقادیر ذاتی) مربوط به ماتریسها و عملگرها از جمله اساسیترین و ذاتیترین، و به همین جهت، پرکاربردترین مباحث و ابزار در بسیاری از زمینهها و میدانهای علوم و فنون قدیم و جدید میباشد.
فضای برداری با بعد متناهی
مسأله اول در مورد فضاهای برداری با بعد متناهی است. ماتریس مربعی  را در نظر میگیریم. بردار غیر صفر
را در نظر میگیریم. بردار غیر صفر  را بردار ویژه
را بردار ویژه  ، و اسکالر
، و اسکالر  را مقدار ویژه نظیر آن بردار میگوییم، چنانچه معادله ماتریسی زیر اقناع شود:
را مقدار ویژه نظیر آن بردار میگوییم، چنانچه معادله ماتریسی زیر اقناع شود:

در معادله ماتریسی حاضر دو مجهول وجود دارد: بردار ویژه  و مقدار ویژه
و مقدار ویژه  . پس حل یکتایی برای آن وجود ندارد.
. پس حل یکتایی برای آن وجود ندارد.
مثال:
ماتریس زیر را در نظر میگیریم:
معادله ماتریسی بالا خواهد شد:
ابتدا معادله را به صورت همگن درآورده و بردار 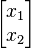 را که قرار است بردار ویژه ما باشد در فاکتور قرار میدهیم:
را که قرار است بردار ویژه ما باشد در فاکتور قرار میدهیم:
در واقع ما از ماتریس همانی (یکه) دوبعدی بهخاطر حفظ طبیعت ماتریسی جملهها استفاده کردهایم. پس از ضرب  در ماتریس همانی و تفریق دو ماتریس داریم:
در ماتریس همانی و تفریق دو ماتریس داریم:
معادله ماتریسی حاصل حالتی خاص دارد. به منظور مقایسه و جهت وضوح در ادامه، معادله اسکالر بسیار ساده زیر را در نظر میگیریم:
که در اینجا  عددی ثابت است. متغیر مجهول
عددی ثابت است. متغیر مجهول 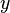 ، تنها و تنها، زمانی جواب غیر از صفر اختیار میکند که داشته باشیم:
، تنها و تنها، زمانی جواب غیر از صفر اختیار میکند که داشته باشیم:
که در این صورت، هر عددی جواب این معادله است.
برای معادله ماتریسی هم درست همین حالات را داریم. یعنی، برای وجود جوابهای غیر صفر به بردار ویژه 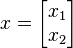 لازم است که دترمینان ماتریس ضرایب صفر شود، و اقناع همین شرط است که به شکلیابی معادله مشخصه ماتریس
لازم است که دترمینان ماتریس ضرایب صفر شود، و اقناع همین شرط است که به شکلیابی معادله مشخصه ماتریس  میانجامد. پس، داریم:
میانجامد. پس، داریم:
با حل این معادله درجه دوم دو جواب زیر برای دو مقدار ویژه ماتریس مفروض بهدست میآیند:
نکات و اشارات
تجزیه مقادیر ویژه را میتوان تکنیکی بسیار مؤثر و قوی در تبدیل پیچیدگی به سادگی دانست. با نگاهی دقیق به این معادله میشود رمز این توانائی را تا حدودی دید:
ضرب ماتریس  در بردار
در بردار  در سمت چپ (عملی سنگین) به ضرب تنها و تنها یک اسکالر ساده در همان بردار (عملی سبک و سریع) در سمت راست تقلیل یافته است.
در سمت چپ (عملی سنگین) به ضرب تنها و تنها یک اسکالر ساده در همان بردار (عملی سبک و سریع) در سمت راست تقلیل یافته است.
فضاهای بینهایت بعدی
توابع پیوسته ریاضی را میتوان بردارهایی با تعداد بینهایت مؤلفه در نظر گرفت، که در فضایی بینهایت بعدی جای گرفته باشد. عملگرهای قابل اعمال بر اینگونه بردارها هم بینهایت بعدی بوده و استفاده از مقدار ویژههای آنها نقشی کارسازتر و پراهمیتتر به خود میگیرد.
عملگر مشتقگیری
به عنوان یک مثال ساده و بسیار پر استفاده، عملگر مشتقگیری از توابع مشتقپذیر ریاضی را در نظر میگیریم:

در این جا عملگر 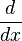 بر روی تابع مشتقپذیر
بر روی تابع مشتقپذیر 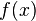 عمل نموده و تابع
عمل نموده و تابع 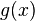 را به دست داده است.
را به دست داده است.
مقدارهای ویژه مرتبط با آن به همان صورتی که در مورد ماتریسها دیدیم معرفی میشوند:

در اینجا به سبب بینهایت بودن بعد فضا، به جای بردار ویژه، عبارت تابع ویژه را داریم. در واقع در جستجوی توابعی هستیم که مشتق مرتبه اول آنها مضربی از خودشان است. با اندکی توجه در مییابیم که عمومیترین پاسخ در اینجا عبارت است از:

چرا که داریم:
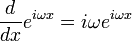
از همین نقطه است که مهمترین و فراگیرترین تبدیل فیزیک ریاضی — تبدیل فوریه — تولد مییابد.




 با میانگین تجربی صفر، که هر سطر یک مجموعه مشاهده و هر ستون دادههای مربوط به یک شاخصه است، تحلیل مولفههای اصلی به صورت زیر تعریف میشود:
با میانگین تجربی صفر، که هر سطر یک مجموعه مشاهده و هر ستون دادههای مربوط به یک شاخصه است، تحلیل مولفههای اصلی به صورت زیر تعریف میشود:
 تجزیه مقدارهای منفرد ماتریس
تجزیه مقدارهای منفرد ماتریس  تشکیل شده است که هر کدام به صورت ستونی در ماتریس قرار داده شده است. بنابرین با توجه به ابعاد بردارها (M) ماتریس دادهها به صورت
تشکیل شده است که هر کدام به صورت ستونی در ماتریس قرار داده شده است. بنابرین با توجه به ابعاد بردارها (M) ماتریس دادهها به صورت  است.
است.![u[m]=\frac{1}{N}\sum^{N}_{i=1}{X[m,i]}](http://upload.wikimedia.org/math/4/6/e/46e2db0b9336e9e61fb19691ff7bf2da.png)

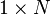 با مقدار ۱ در هرکدام از درایهها است.
با مقدار ۱ در هرکدام از درایهها است. به صورت زیر به دست میآید:
به صورت زیر به دست میآید:![C=\mathbb{E}[B\otimes B]=\mathbb{E}[B\cdot B^{\ast}]=\frac{1}{N}B\cdot B^{\ast}](http://upload.wikimedia.org/math/5/0/c/50c241be5d8692a9b08d288293bda0c5.png)
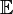 میانگین حسابی است.
میانگین حسابی است. ضرب خارجی است.
ضرب خارجی است. ماتریس ترانهاده مزدوج ماتریس
ماتریس ترانهاده مزدوج ماتریس  است.
است. ، به دست میآید.
، به دست میآید.
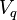 در ستون qام قرار دارد و مقدار ویژه qام یعنی درایهٔ
در ستون qام قرار دارد و مقدار ویژه qام یعنی درایهٔ  متناظر با آن است. بازچینی بردارهای ویژه بر اساس اندازهٔ مقادیر ویژه متناظر با آنها صورت میگیرد. یعنی بر اساس ترتیب کاهشی مقادیر ویژه، بردارهای ویژه بازچینی میشوند. یعنی
متناظر با آن است. بازچینی بردارهای ویژه بر اساس اندازهٔ مقادیر ویژه متناظر با آنها صورت میگیرد. یعنی بر اساس ترتیب کاهشی مقادیر ویژه، بردارهای ویژه بازچینی میشوند. یعنی 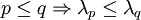

 انتخاب میشود. در اینجا میتوان از انرژی تجمعی استفاده کرد که طبق آن
انتخاب میشود. در اینجا میتوان از انرژی تجمعی استفاده کرد که طبق آن![g[m]=\sum_{q=1}^m{\lambda_q}](http://upload.wikimedia.org/math/0/f/f/0ffcd51a85da753ef5957da5f814ec00.png)
![g[m=l] \leq 90%](http://upload.wikimedia.org/math/0/a/1/0a1298560bae33fd6440eae1b50e626c.png)
![W[p,q] = V[p,q], p=1\dots M ,q = 1\dots l](http://upload.wikimedia.org/math/3/c/7/3c704fbbc9ab643526f2c54b4e932713.png)
 انحراف معیار مجموعه داده است که میتواند به صورت زیر به دست بیاید:
انحراف معیار مجموعه داده است که میتواند به صورت زیر به دست بیاید:![s[i] =\sqrt{C[i,i]}](http://upload.wikimedia.org/math/0/8/6/086f1df445a97de8439854dcf5c631cc.png)
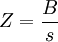 ‘
‘
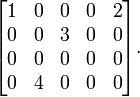


 را در نظر میگیریم. بردار غیر صفر
را در نظر میگیریم. بردار غیر صفر  را بردار ویژه
را بردار ویژه  را مقدار ویژه نظیر آن بردار میگوییم، چنانچه معادله ماتریسی زیر اقناع شود:
را مقدار ویژه نظیر آن بردار میگوییم، چنانچه معادله ماتریسی زیر اقناع شود:


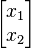 را که قرار است بردار ویژه ما باشد در فاکتور قرار میدهیم:
را که قرار است بردار ویژه ما باشد در فاکتور قرار میدهیم:
 در ماتریس همانی و تفریق دو ماتریس داریم:
در ماتریس همانی و تفریق دو ماتریس داریم: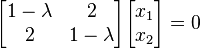

 عددی ثابت است. متغیر مجهول
عددی ثابت است. متغیر مجهول 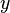 ، تنها و تنها، زمانی جواب غیر از صفر اختیار میکند که داشته باشیم:
، تنها و تنها، زمانی جواب غیر از صفر اختیار میکند که داشته باشیم:
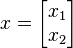 لازم است که دترمینان ماتریس ضرایب صفر شود، و اقناع همین شرط است که به شکلیابی معادله مشخصه ماتریس
لازم است که دترمینان ماتریس ضرایب صفر شود، و اقناع همین شرط است که به شکلیابی معادله مشخصه ماتریس 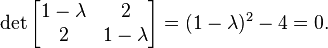


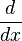 بر روی تابع مشتقپذیر
بر روی تابع مشتقپذیر 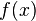 عمل نموده و تابع
عمل نموده و تابع 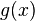 را به دست داده است.
را به دست داده است.